david's pl notes

denotational semantics and domain theory

Sep 02, 202415 min read

This is a note on denotational semantics, undergirded by an extended exploration of domain theory, which provides the theoretical underpinning for the former.

References

This explanation incorporates notes from the following sources:

For a basic definition of and explainer of denotational semantics, see Winskel 5: The denotational semantics of Imp and this other StackExchange answer. These notes onwards go over dealing with recursive constructs in denotational semantics with domain theory and partial orders.

Dealing with recursive constructs

In A denotational semantics for IMP, we defined the denotation for while in terms of a recursive equation, that we resolved by finding the fixed point of operators on sets—in this case, the fixed point of repeated set unions. In particular, we defined an operation that returns the value of for some while expression after iterations, given the value of after iterations.

The proof for showing that such a fixed point exists at all involves showing that every time we call , the set we get back is either equal to or a superset of . Since our sets actually represent functions, this means that given , must be defined on more inputs than is; if , then or (i.e., the function is undefined on that input). You could also say that has more information than , since it’s defined on more inputs. Since the solution is the (minimal) fixpoint of this operation, we can say that the solution is whatever function the set represents that contains more information than and and and …

In this case, we could get away of seeing the semantics of while as the fixed point of doing a bunch of set unions. However, this will not always be possible:

In Section 5.4 we shall introduce a general theory of fixed points, which makes sense when the objects defined recursively are not sets ordered by inclusion.

More generally, we’re not just interested in sets. What we’re actually interested in is some notion of some function having more or less information than another function. And actually since the denotation of some syntax might be any mathematical object, not just a function, we’re interested in the general notion of a mathematical object having more or less information than another object.

This general notion of information-having is a partial ordering, which is defined and dealt with in a branch of abstract math called domain theory. Domain theory gives us the language to generalize the idea of “using fixpoints to find sets that denote recursive constructs” beyond just sets, but to any mathematical object that might denote some construct in a language of our choosing. The lecture notes summarize the key insight behind this perspective:

The key idea is to consider a partial order between the mathematical objects used as denotations—this partial order expresses the fact that one object is approximated by, or carries more information than, or is more well-defined than another one below it in the ordering. Then the minimal solution of a fixpoint equation can be constructed as the limit of an increasing chain of approximations to the solution. (Lecture notes, 4)

Basically, we create a partial ordering between functions that provides mathematical structure for this intuition of “having more information.” Then, we create a chain of partial orderings (analogous to the business from before) corresponding to increasing recursive iterations. Finally, in the limit, this will approach some minimal set that has more information than all the recursive calls in the chain. This definition doesn’t rely on set operations, but on a more general operation (partial ordering) that operates on functions and other “mathematical objects” that we deal with in denotational semantics.

Partial orders in the abstract

First, let’s define partial orders in the abstract. This won’t have much meaning for now, but trust me, we’ll see how these operations become useful and can become imbued with meaning in the next sections. Like monads!

A partial order on a set is an operation that must fulfill three key properties:

  • Reflexivity:
  • Transitivity:
  • Anti-symmetry:

Domain theory in a worked example

Let’s walk through how we might find the denotation for a while loop that calculates the factorial of a number n:

x = n
y = 1

while x > 0:
	y = x * y
	x = x - 1

In this case, our state is a pair , and the denotation of this while loop is a function from pairs of integers to pairs of integers. Let’s define a function that takes a state function and returns a new state function:

This function is analogous to from the Winskel 5: The denotational semantics of Imp notes. We’re trying to find a state function such that . For notation, we define as:

Basically, is the denotation of the while loop after a maximum of iterations. For example, with just one evaluation of the condition of the while loop, we can only return a result if x is already 0:

This is because we can’t call , but we can return a result. With max one run of the loop body, we can return a result if is 0 or 1:

And so on. In general, we have:

Bringing back partial orderings

If we’re looking at these functions, we can intuit that has more information than if . We encode this notion in the partial ordering operator. The partially ordered set (i.e., poset) of state functions consists of the underlying set of state functions and the operation. For these functions, if and only if:

In other words, must be defined in at least all the places is, and must have the same values that has. However, can be more defined.

Let’s do some more abstract definitions. Given a poset and a subset , an element is the least element of if . Because is anti-symmetric, has at most one least element. Additionally, the least element of a subset might not exist! The least element of the whole set is the bottom element of a set, written for a set , or just when the set can be inferred.

A countable, increasing chain in a poset is a sequence of elements of satisfying:

These elements do not have to necessarily be distinct! It could be one element repeating forever if we wanted to.

An upper bound for the chain is any where . if it exists, the least upper bound (i.e., lub) is written as:

Our definition of above is the lub of the chain of functions !

A complete partial order (i.e., cpo) is a poset where every chain has a lub. For instance, the poset isn’t a cpo, since there’s no lub for the chain .

A domain is a cpo with a bottom element. i.e., it’s not just that every chain has a lub, but the whole set has an element that is “smaller than or equal to” all others. Hence, domain theory!

Now, let’s start talking about functions operating on cpos, like our function above! A function between cpos and can have several properties:

  • Monotonicity: the function preserves partial ordering.

  • Continuity: for all chains in , the lub of function calls of elements in a chain is the same as calling the function on the lub.

  • Strictness: if and have least elements, then must return when passed :

Example

Let’s consider the domain of natural numbers with an additional “top” element . If we define a function , it’s monotonic (, and ) and strict, but isn’t continuous. Consider the chain consisting of all natural numbers (but not itself) The lub of the chain of all natural numbers is straightforwardly , so . However, when evaluating , will always return (infinity is weird). Thus, we have , and .

Tarski’s fixed point theorem

A fixed point of a function is an element such that .

The pre-fixed point of a function on a poset is an element s.t. . Note that the function application is on the left side; the result of applying will be “less” than the argument. The least pre-fixed point of , if it exists, is written . This least pre-fixed point will have two properties:

  • (by definition, set )
  • (since the fixed point is on the left side)

It’s important to note that the least pre-fixed point its itself a fixed point: (the proof is in Lecture notes p. 16). It is thus the least of all fixed points of .

Tarski’s fixed point theorem states that a continuous function on a domain will have a pre-fixed point with the following definition:

Additionally, since is a fixed point of , so it is the least fixed point of .

This theorem allows us to give denotational semantics for programs with recursive features! We can prove that a recursive function has a fixed point if it’s continuous and operating on any domain , which our set of state functions is (I’m not showing that here I’m tired).

Go team!

Domain theory, and operations therein

Now, we take a more abstract lens, focusing on domain theory. Let’s start with denotational semantics’ connection to domains:

In denotational semantics a programming construct (like a command, or an expression) is given a meaning by assigning to it an element in a “domain” of possible meanings. The programming construct is said to denote the element and the element to be a denotation of the construct. For example, commands in IMP are denoted by elements from the “domain” of partial functions, while numerals in IMP can denote elements of . (Winskel 119)

And why do we need domain theory and, in particular, partial orders?

As the denotational semantics of IMP in Chapter 5 makes clear it can sometimes be necessary for “domains” to carry enough structure that they enable the solution of recursive equations. (Winskel 119)

Winskel §8 continues with redefinitions of cpos, monotonicity, and continuity. When we want to use domains for expressing (recursive) programming constructs, we want cpos and monotonic, continuous functions on those cpos, since recursive constructs can only be expressed in terms of cpos.

Isomorphisms

Before we get going, we quickly formally define an isomorphism. Given two cpos and , a function is an isomorphism iff is a 1-1 correspondence such that

This is monotonicity across domains. Basically, if an isomorphism exists between and , they are isomorphic and are basically “equivalent” down to renaming.

Discrete domains

A discrete cpo is a set where the partial ordering relation is the identity. A chain of partial orderings is just the same element repeated over and over again. Basic values—bools, ints—form discrete cpos. Any function from a discrete cpo to another cpo is continuous.

Products

Let be cpos. The underlying set of their product is:

which consists of -tuples for .

The partial ordering operation is done element-wise:

Lubs of chains are also calculated componentwise. The product of cpos is a cpo.

The projection function is continuous.

We can tuple functions too. Given , we can define the function:

This function is monotonic.

We can define the product of functions . This is continuous.

Properties on general functions on products

  • If is a function from a cpo to a product of cpos, it’s monotonic/continuous iff is monotonic/continuous for all .
  • If is a function from a product of cpos to a cpo, it’s monotonic/continuous iff it’s monotonic/continuous in each argument separately (i.e., with respect to each argument, while keeping others constant).
  • This basically let’s us do commutativity:

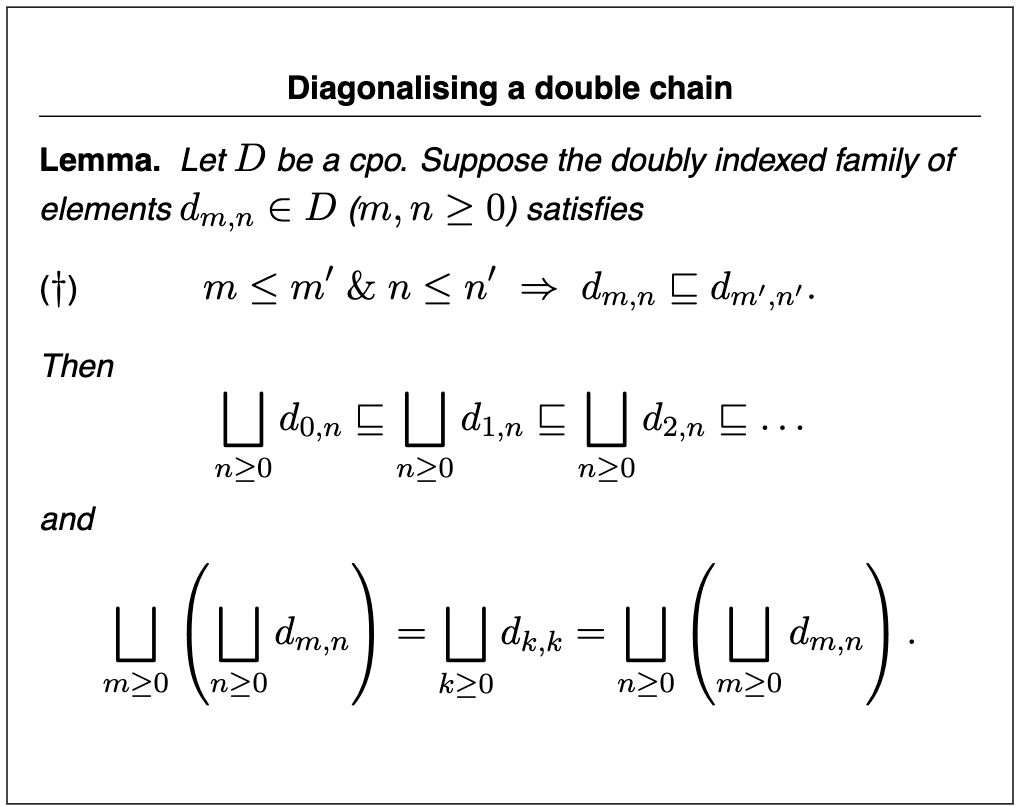
Functions

The set of continuous functions of type between two cpos is a cpo! This set is written as , and partial ordering is defined as:

Application and currying are continuous. The fixpoint operator is continuous.

Flat domains

To model ground types like and , we use flat domains, which is a discrete domain augmented with a bottom value . Formally, given some discrete cpo , let . Then, we define partial ordering as:

Thus, . This is also called a lifted cpo by Winskel §8.

Sums

Finally, we can form disjoint unions of cpo’s. Let be cpos. A sum is defined by the set:

and partial order

This relies on injection functions which are 1-1 such that

We can combine into a single continuous function:

TODO

There are lots of proofs that I’m eliding here, particularly proofs of function continuity and monotonicity. Be wary.

Graph View

Backlinks