Summary
Evaluation styles Call-by-name: no reductions inside abstractions. Lazy. Call-by-value: outermost redexes reduced, redex reduced only if right-hand side is a value. Strict.
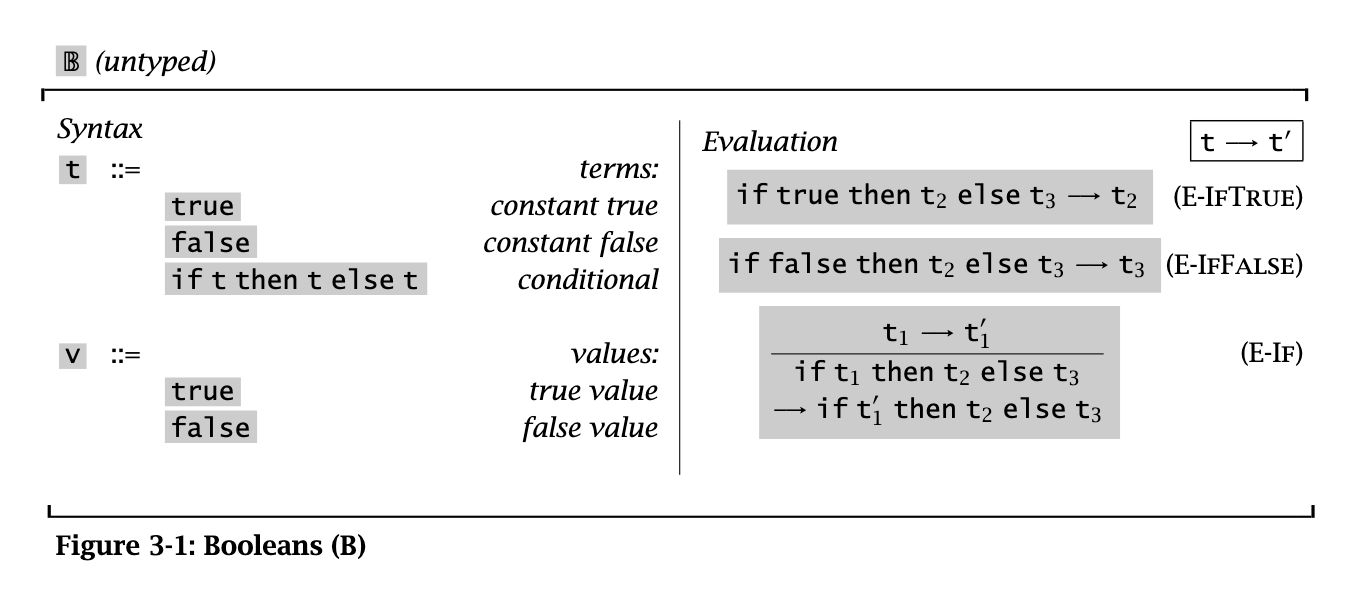
§ 3. Syntax & semantics
Syntax
Can be defined inductively: “the set of terms is the smallest set
Can also be defined using inference rules. Read as: “if we have established the statements in the premise(s) listed above the line, then we may derive the conclusion below the line.”
Concretely, you can define the set of terms in terms of iteratively building sets:
You can do structural induction on terms this way (think pattern matching on ADTs in Haskell). This is commonly how induction on terms goes.
Induction on syntax
Three kinds:
- Induction on depth: show
given - Induction on size: show
given - Structural induction: show
given for all immediate subterms of .
Normally you do case-by-case based on variant of term.
Semantics
Three kinds:
- Operational: Specify an abstract (i.e., operates directly on language terms, not assembly or whatever) machine with state and transition function. Meaning of a term is final state of machine when it starts with that term.
- There are many possible operational semantics!
- Denotational: A term’s meaning is a mathematical object, like a number or function. A denotational semantics is finding a collection of semantic domains and an interpretation function that goes from terms to these semantic domains. Domain theory is the research of finding appropriate semantic domains.
- Lets you find laws about programs—that programs have same behavior, that some things are impossible in a language
- Axiomatic: state these laws as the definition of the language itself. The meaning of a term is what can be proved about it
- Invariants come from this view.
Evaluation
- A rule is satisfied by a relation if:
- For every instance of rule, conclusion in relation or a premise is not.
- Evaluation relation
: “ tevaluates tot'in one step.”- The evaluation relation is the smallest binary relation that satisfies some set of evaluation rules.
- If
is in this relation, then “the evaluation statement/judgment is derivable” - i.e., we can build a derivation tree to get

- This isn’t the same as multi-step eval
!
- i.e., we can build a derivation tree to get
- Terms evaluate to values.
- All terms are values. The term syntax should include values.
- Normal form: most evaluated form.
- All values are in normal form, but not all normal forms are values (e.g., errors)
- Non-value normal forms are stuck. ^9c29eb
- Run-time error!
- Small-step v. big-step
- In big-step semantics, we directly say “the term
evaluates to a final value ”: - For instance, the rule big step rule
B-IfTruecorresponding toE-IfTruewould be:
- In big-step semantics, we directly say “the term
§ 5. Untyped lambda calculus
- Why do we care about lambda calculus?
- You can use it to describe all computation
- But it’s simple enough to make proofs about programs
- Abstract and concrete syntax
- Concrete/surface syntax is what the user writes
- An AST reprs the program as a labeled tree.
- Concrete transformed by lexer (gets tokens, ignores whitespace) and parser (turns tokens into AST)
- A closed term (aka combinators) are terms that contain no free variables.
- Operational semantics: var subst!
- Redex: “reducible expression”
- Beta reduction: fn eval
- Alpha conversion: rename args
- Different evaluation strategies:
- Full beta-reduction: any redex can be reduced at any time
- Normal order: leftmost, outermost redex first
- Call-by-name: no reductions inside abstractions. Lazy.
- Call-by-value: outermost redexes reduced, redex reduced only if right-hand side is a value. Strict.
- Multiple args via currying
- Church booleans:
- True:
- False:
- Apply booleans to two values to do conditional selection. First element if true, second if false.
- True:
- A pair passes two values into a boolean function.
fstpasses in true,sndpasses in false - Church numerals: a number
is a function that applies a function to a value , times - Math proceeds as it did in CSE 230 lmao
- Recursion
- The
omegacombinator evaluates to itself:omega = (λx. x x)(λx. x x) - The fixed-point combinator lets us
fix = λf. (λx. f (λy. x x y)) (λx. f (λy. x x y))
- The
- Substitution
- Variable capture: free variables in a term becoming bound b/c of naive substitution
- In an abstraction, we don’t want to subst such that a free var becomes bound or vice versa.
- Subst rule captures this intuition:
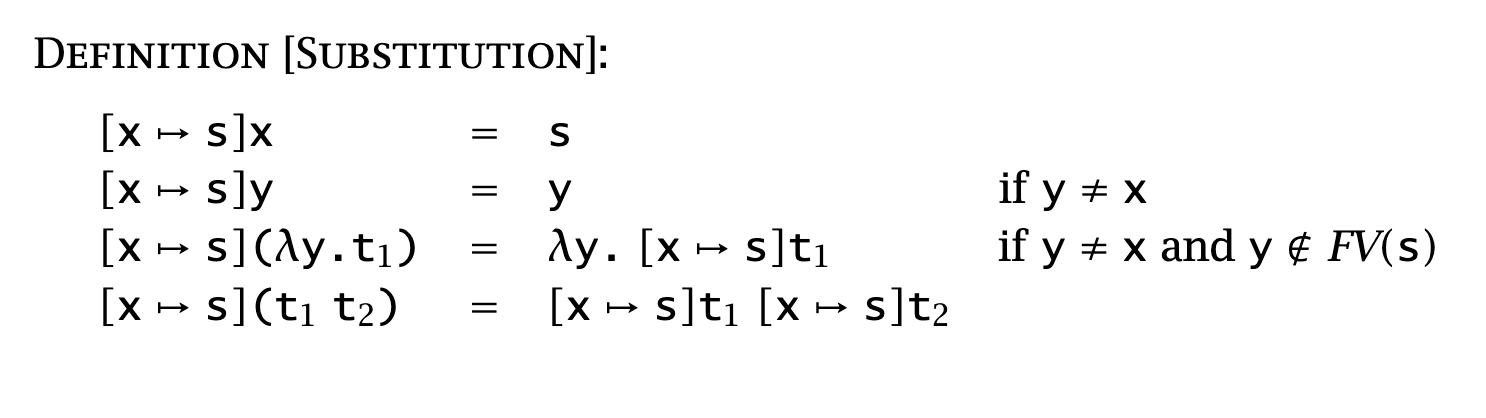
- Normally our subst rules should be capture-avoiding substitutions.
- Variable capture: free variables in a term becoming bound b/c of naive substitution
- Operational semantics
- We can formulate our operational semantics to do different eval strategies!
-
With full beta-reduction, there is no order, so we can have overlapping eval strats:
-
-
- Or, we can require values in certain positions of our eval rules, to enforce diff eval strat.
§ 6. de Brujin indices, briefly
i.e., nameless representation of vars.
A bound variable is represented by how many levels up the lambda that binds this variable is.
To represent free variables, our naming context
Thus,
We define a shift operator