pierceTAPL11Simplytyped2002

§ 8. Typed arithmetic expressions

Also recall:

Transclude of pierceTAPL2002#^9c29eb

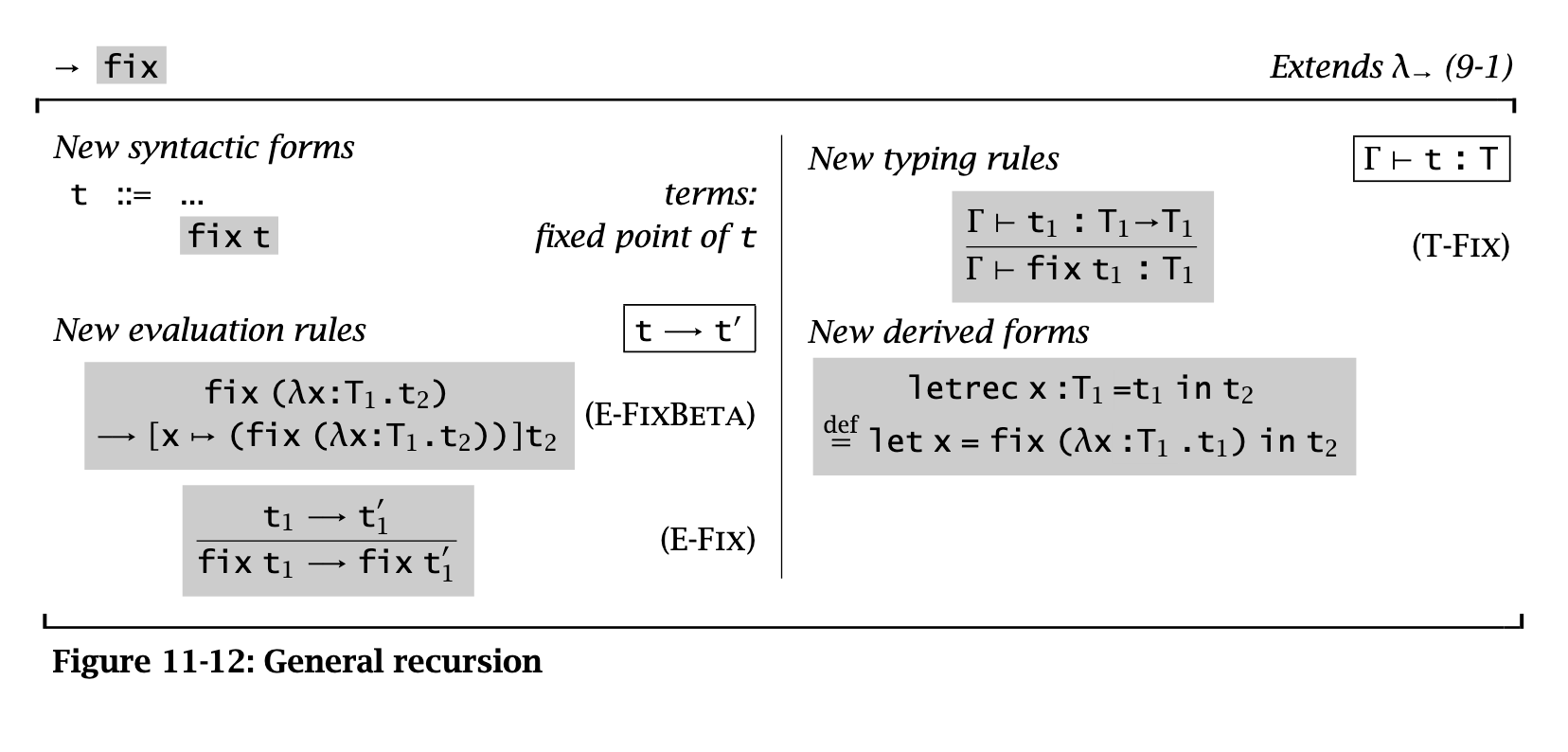
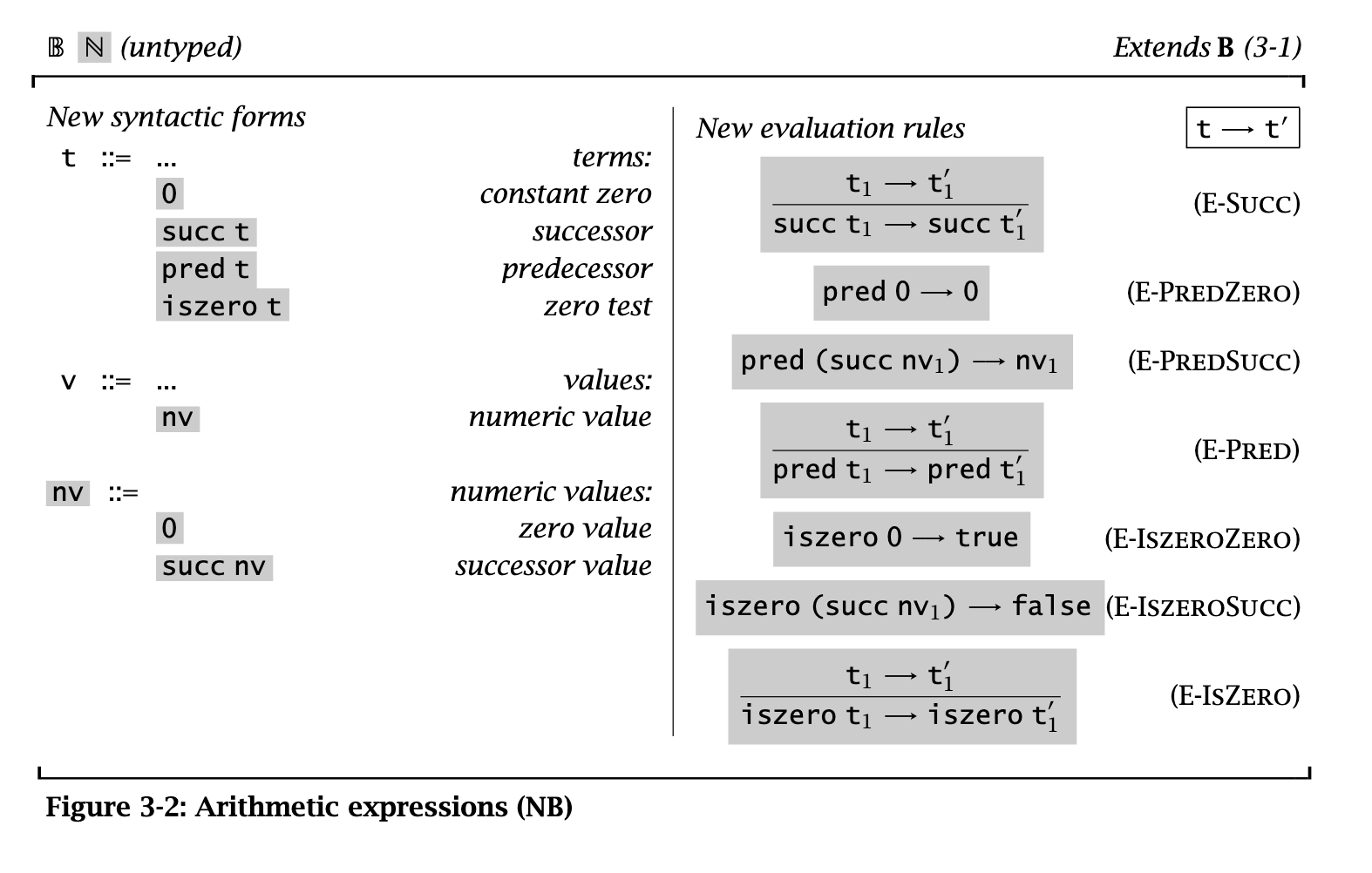
How can we figure out stuck terms (e.g., pred false) without evaluation? For one, we should distinguish between booleans (Bool) and natural numbers (Nat)!

The typing relation

Definition

The typing relation means that has type . This relation is defined using inference rules, like with evaluation.

• A term is well-typed if .
• The typing relations go from smaller to bigger, for instance:

- Inversely, we can derive lemmas that "invert" this relation, for instance, if `if t1 then t2 else t3 : R`, then the statements `t1 : Bool`, `t2, t3 : R` hold.
- These are *generation lemmas* - they show how to calculate the types of terms!
- These generation lemmas are what we use when building type-checkers are stuff. The derivation rules operate "backwards" to how a type-checker would operate.

• “statements (aka judgments) are formal assertions about the typing of programs, typing rules are implications between statements, and derivations are deductions based on typing rules”

• Uniqueness of types: each term has at most one type, and one derivation.
  • This is not true in the general case (e.g., subtyping)

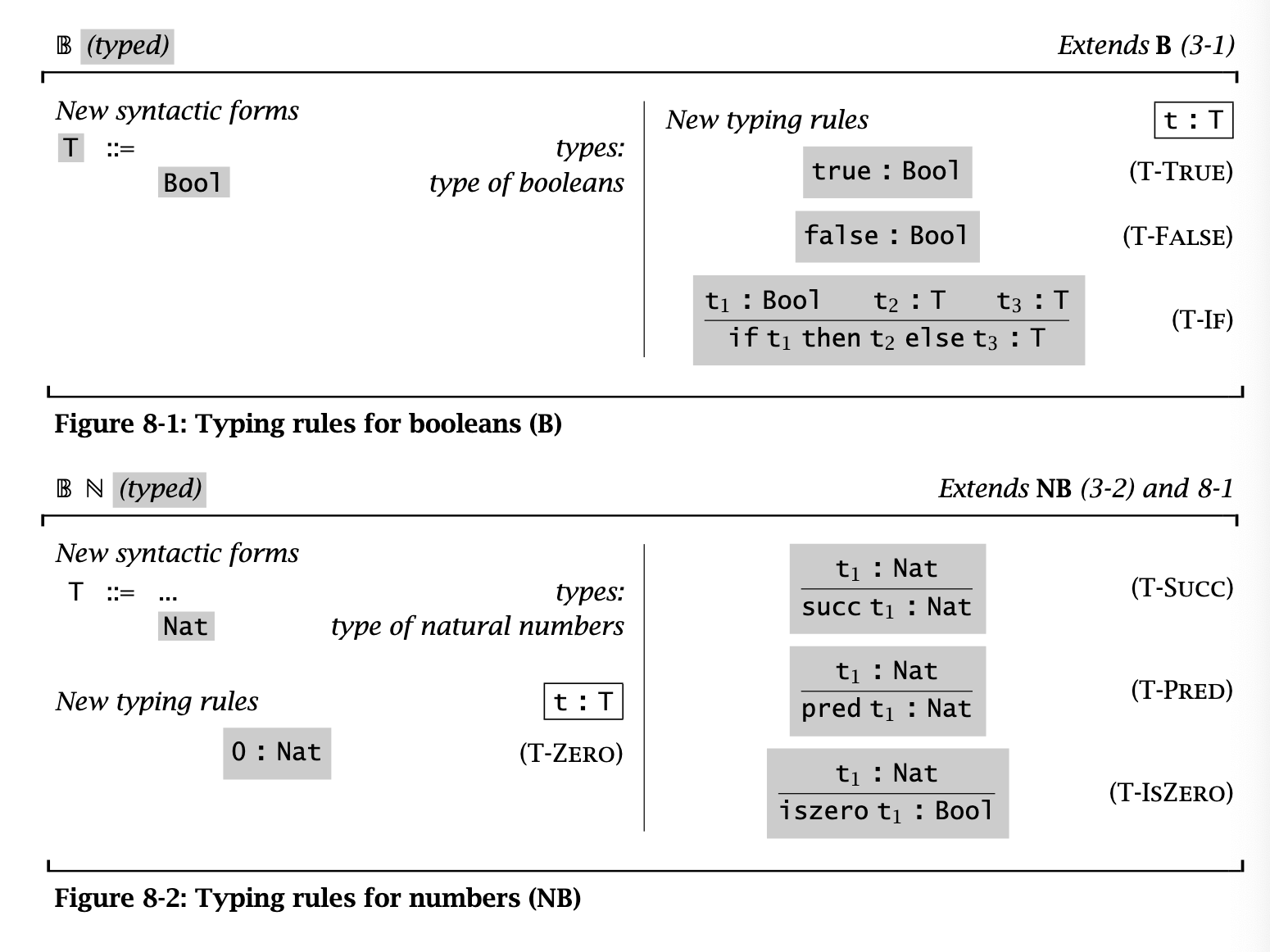
Here are the typing rules for the arithmetic expr lang:

Type safety = progress + preservation

Definition

What is type safety? Type safety is the property that well-typed terms do not get stuck. We do this basically via induction, using two steps:

• Progress: A well-typed term is not stuck—it’s either a value or can take an evaluation step
• Preservation (aka subject reduction): If a well-typed term takes an evaluation step, the resulting term is also well-typed.
  • The resulting term doesn’t necessarily need to have the same type (e.g., in subtyping), but for this example, it should.

To help with proofs, we define the canonical forms of our types—the well-typed values of these types. Think of these like the ADT definition:

data Bool = True | False
data Nat = Z | Succ Nat

Progress proof for arithmetic exprs

Eval rules

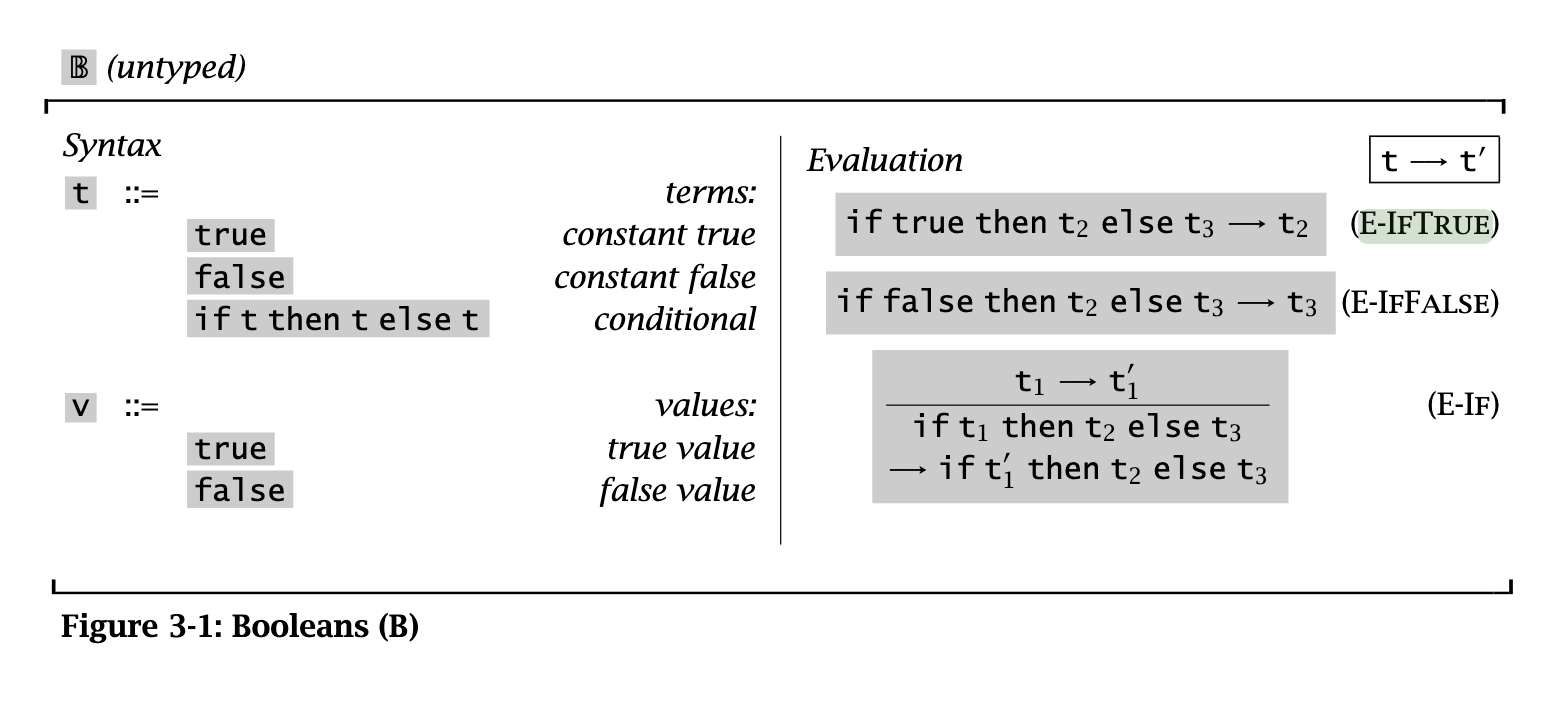
By the structure of the progress proof, let’s assume that . We want to show that is a value, or .

We proceed with induction on the derivation of . The last step of ‘s derivation can be one of a number of possibilities:

• In T-True, T-False, and T-Zero, is a value, so we’re done.
• For T-If, by the induction hypothesis, either is a value or .
  • If is a value, it must be one of the canonical forms for Bool, meaning either E-IfTrue or E-IfFalse applies.
  • If , E-If applies.
  • In either case, an eval step exists.
• For T-Succ, by the induction hypothesis, is a value or can evaluate to .
  • If it’s a value, by the canonical forms lemma, succ t1 is also a value (i.e., value by construction)
  • Otherwise, E-Succ applies.
• For T-Pred, by the induction hypothesis, is a value or can evaluate to .
  • If it’s a value, by canonical forms lemma, it’s either 0 (E-PredZero) or succ nv1 (E-PredSucc)
  • Otherwise, E-Pred applies.
• Same for T-IsZero.

Preservation for arithmetic

Let . We want to show if and , then .

Again, we do induction on a derivation of . We assume preservation holds for subderivations of the current derivation—at any point, if proving preservation involves looking at a subterm that is well-typed () and evaluates to , we assume the induction hypothesis (preservation) holds for that term . This works by structural induction—if you can show preservation holds for a term given its subterms, you can recurse all the way down to the base case. We do case analysis on the last step of the typing derivation.

• In T-True, t = true and T = Bool. It’s already a value and there’s no , so it’s true.
  • Same reasoning applies for T-Zero.
• In T-If, since we know if t1 then t2 else t3 has type , we also must know that and . Since we know that , there are three possible evaluation rules that could apply at this point.
  • If E-IfTrue applies, and . from the subderivation, so we’re good.
  • If E-If applies, and . By the IH, . Then, by T-If, this whole expr .
• In T-Succ, there are two possibilities.
  • If is already a value, is a value too and there’s no .
  • Otherwise, E-Succ applies and . From T-Succ we know that , and by preservation IH this means . And by T-Succ this means that .

Note

You don’t need to do induction on typing derivations; you can do induction on evaluation derivations too!

• Note that while subject reduction holds, subject expansion doesn’t always hold.
  • Evaluation can “erase” ill-typed terms (see here)
  • For instance, t = if true then 0 else false.
  • By E-IfTrue, t' = 0, and by canonical lemma, t' : Nat.
  • But t is stuck!
• If you’re doing big-step evaluation, swap out with .
• If you have an explicit wrong term that is generated whenever you get stuck, progress must evaluate to a non-wrong term.
  • e.g.,

§ 9. Simply Typed Lambda-Calculus

We’re gonna look at a version of lambda calculus augmented with primitive booleans and conditionals. We have two type constructors: booleans and arrow (functions).

The Typing Relation

First, let’s define the typing context stuff real quick.

Definition

A typing context (aka type environment) is a sequence of variables and their types. The comma operator extends by adding a binding on the right. The empty context can be omitted.

This context can be conceptualized as a set of pairs, and thus a function/relation (with a domain and range) from variables to types.

Let’s look at the typing judgment for abstractions, T-Abs:

This captures the intuitive statement: “if assuming that, among other things, , then we know that the abstraction has type .” One thing you might ask is why not format it like this:

We format it the first way because ‘s type depends on ! They’re not just independent clauses. references , and needs to assume that in its evaluation/typing environment, .

The other typing rules are straightforward.

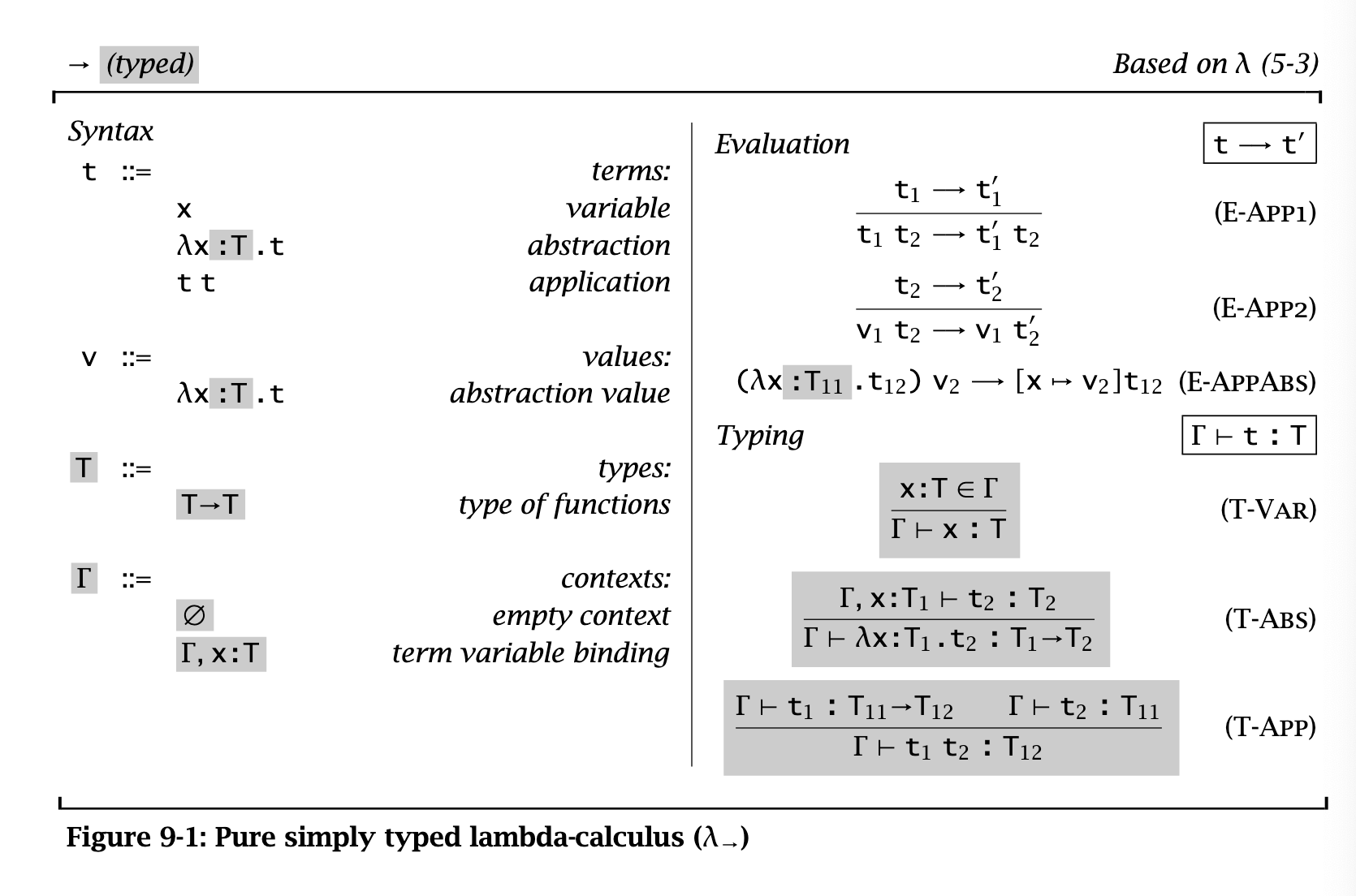
Properties of typing

These are the same lemmas we’ve seen before:

• Inversion: “if a term of this form is well-typed, its subterms must have types of these forms”
  • e.g., if , then and .
  • Reversing the direction of derivations.
• Uniqueness: In a given context , a term with all free variables in must have at most one type.
• Canonical forms:
  • Bools are true or false
  • If , .

Progress for STLC

We only care about proving progress for closed programs with no free variables (i.e., empty context), since complete programs are always closed. Apparently the proof is similar to Progress proof for arithmetic exprs.

Preservation for STLC

Proving preservation requires a few lemmas first:

• Permutation: you can reorder contexts.
• Weakening: if you have a judgment , you can add whatever variables you want to and this still holds.

We also show a more ambitious lemma:

• Preservation under substitution: we want to show that if and , then . ^1b85cb
  • Let’s do case analysis on the first judgment.
    • In T-Var, must be a variable, since maps from variables to types.
      • Either , in which case we already know from the assumptions
      • Or not, in which case no substitution happens and we’re fine.
    • In T-Abs, we can assume and .
      • .
      • We can show by the induction hypothesis
        • We do this by weakening to .
      • Thus, by T-Abs, .
      • By definition of substitution, running the subst on the whole abstraction is the same as running the subst on its body if . So we’re good!
    • etc.

Apparently showing preservation is similar to Preservation for arithmetic at this point.

The Curry-Howard correspondence

• The type constructor has two kinds of typing rules:
  • An introduction rule T-Abs showing how elements of this type can be created
  • An elimination rule T-App showing how elements of this type can be consumed.

Proofs have very computational vibes!

• Proving means finding concrete evidence for .
• Proving means, if you’re given this concrete evidence (i.e., a proof) of , transforming it somehow into concrete evidence of .
• Proving means finding both and .

The Curry-Howard correspondence states as follows:

Logic	PLs
propositions	types
proposition	type
proposition	type
proof of proposition	term of type
proposition is provable	type is inhabited by some term

Girard’s linear logic led to linear type systems!

Erasure and typability

Compilers normally check types at compile time, then erase them at runtime.

Curry-style vs. Church-style

• In Curry-style, we can talk about evaluation of non-well-typed terms. Semantics is before typing.
• In Church-style, evaluation is only defined on well-typed terms. Typing before semantics.

§ 11. Simple Extensions

These extensions (almost) all introduce derived forms—syntax sugar!

Base types

• Strings? Floats? Things with opaque inner workings.
• We consider these as uninterpreted, unknown, or atomic base types, in the set with no primitive operations on them at all.
  • i.e., can’t (de)construct them like nats or anything like that.

Unit type

We add a new constant value and a derived form where .

An aside on derived forms

With derived forms, we can either formalize them as new constructs, or as syntax sugar. To prove that something is a derived form (i.e., is basically syntax sugar), we define an elaboration function that transforms from a more complex language to a simpler language . We then show that evaluation and typing both correspond:

• iff .
• iff .

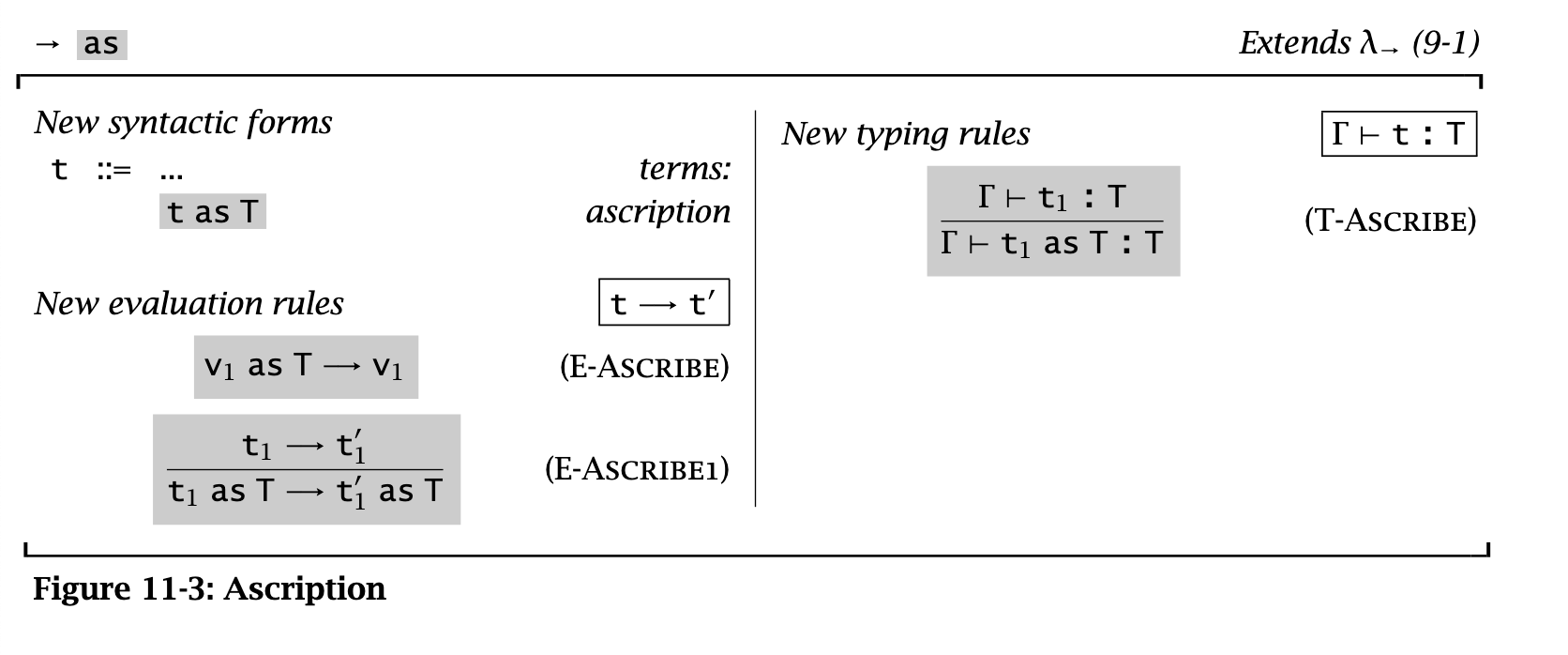
Ascription

Explicitly saying an expression has a type: t as T. Pretty simple.

Let bindings

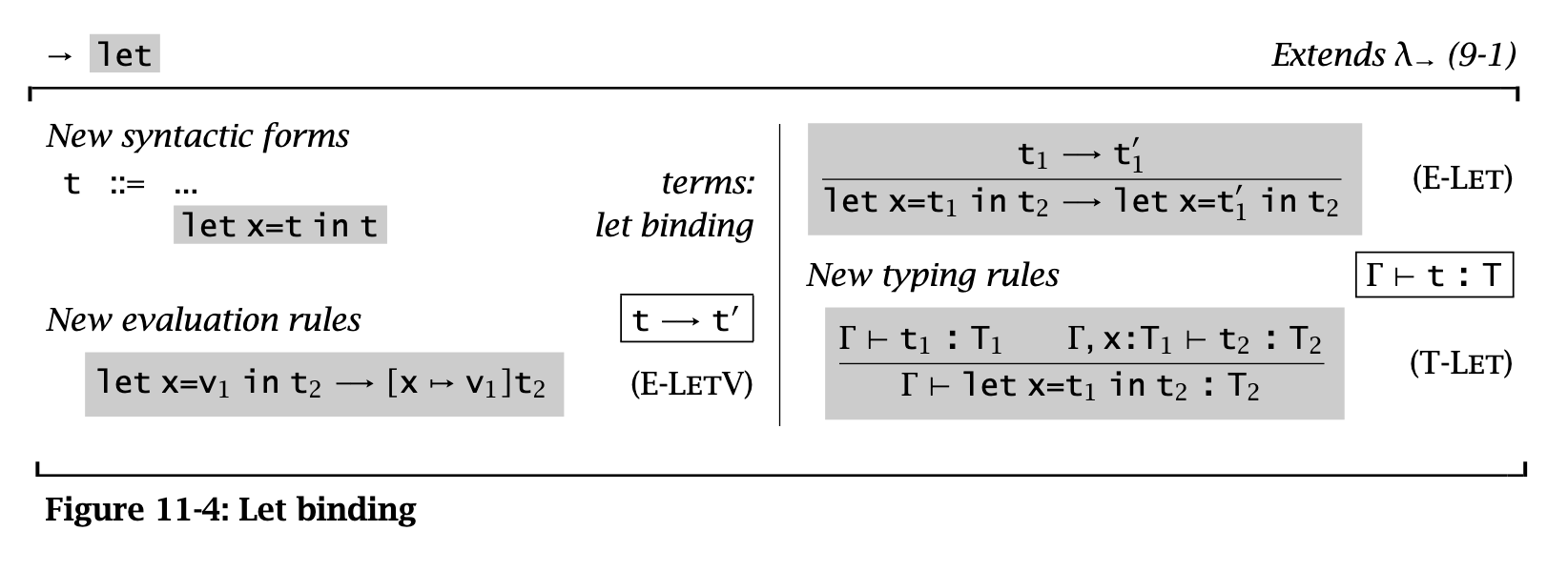
Straightforward. But expressing this as a derived form isn’t so straightforward. Naively, we’d want to do this:

But comes not from the syntax purely, but from the info from the typechecker! So really this isn’t a transformation on terms, but on typing derivations. This derived form transforms a derivation involving let into one that uses abstraction and application:

We could define let as immediate substitution, but this changes eval order and erases ill-typed terms.

Tuples & records

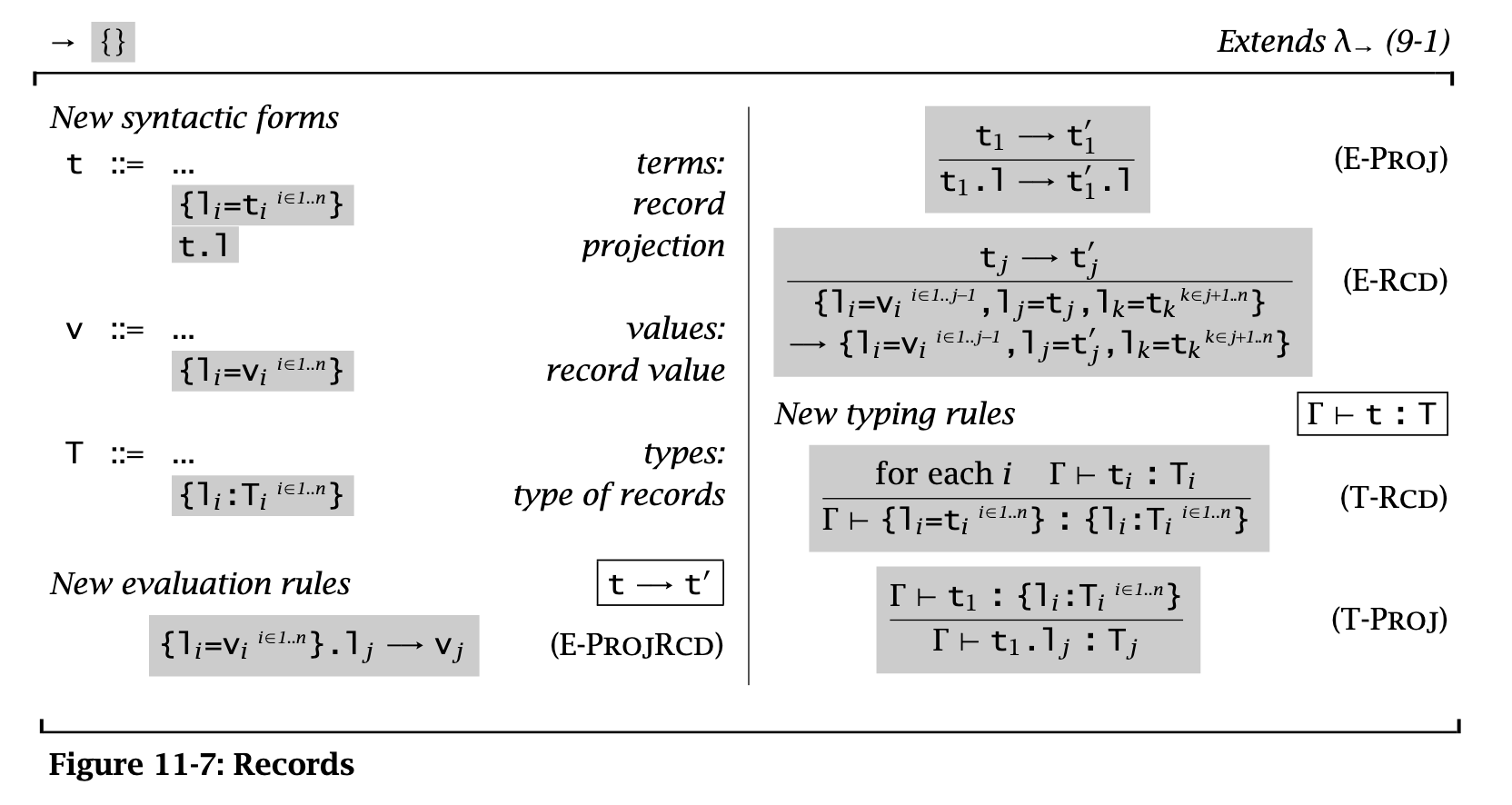
Make note of syntax mostly. Records are the same, except with explicit labels instead of numbered fields.

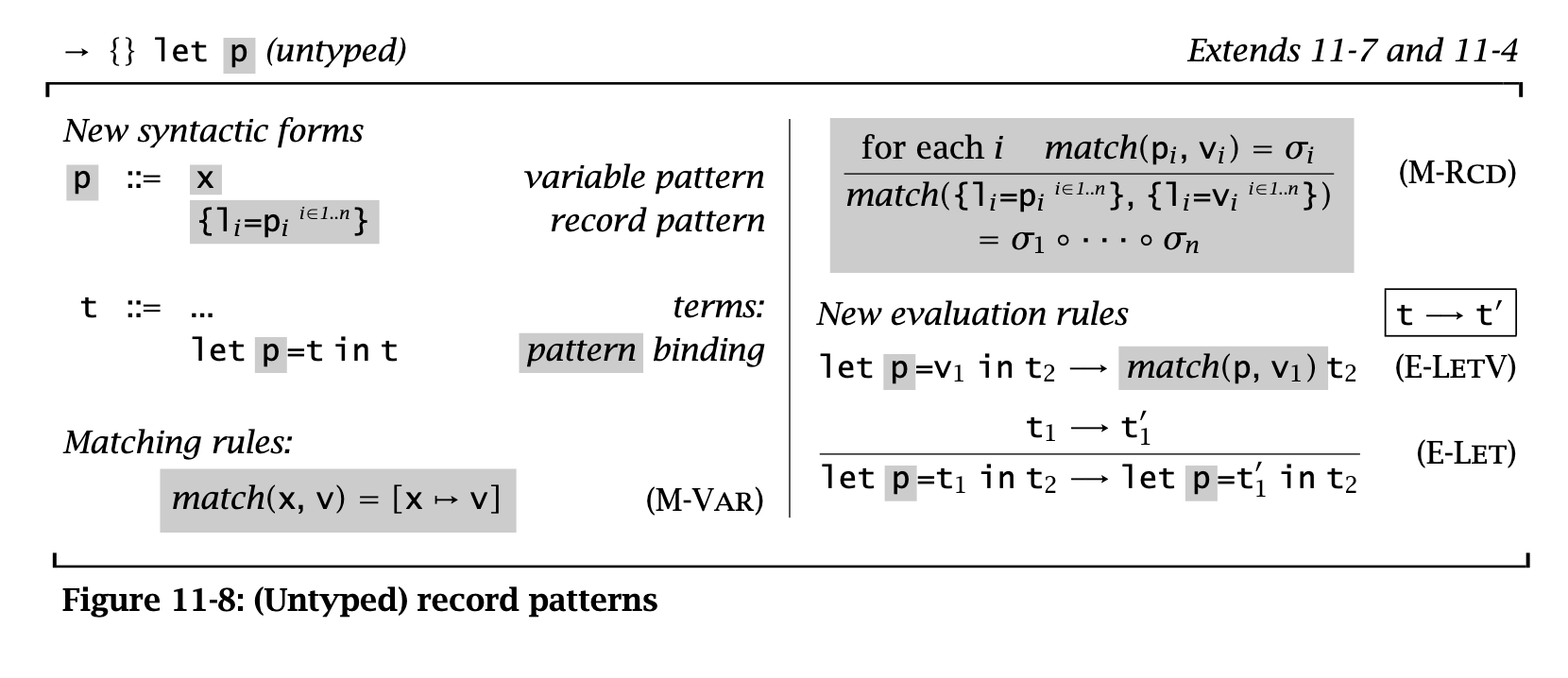
This defines a new match function to generate substitutions through pattern-matched records.

Sums & variants

This is a binary sum type (e.g., data Sum a b = Inl a | Inr b):

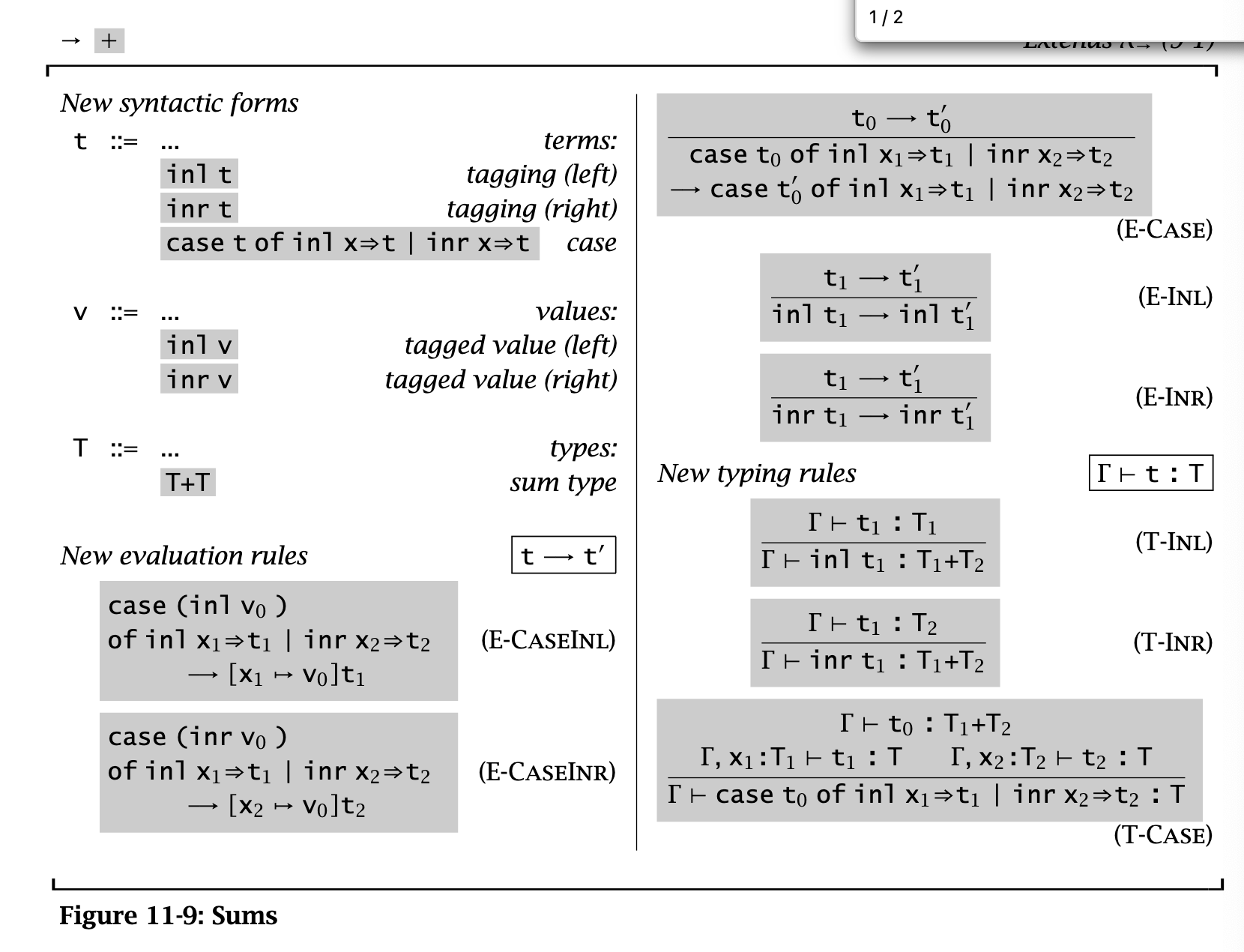
However, sums don’t satisfy uniqueness of types. In T-Inl, can have infinitely many types corresponding to different choices of . We can solve this by either holding it indeterminate and making it concrete later on (type reconstruction), allowing all possible values of to be represented uniformly (i.e., subtyping), or forcing the programmer to ascribe everything lmao.

This is the fully general variants:

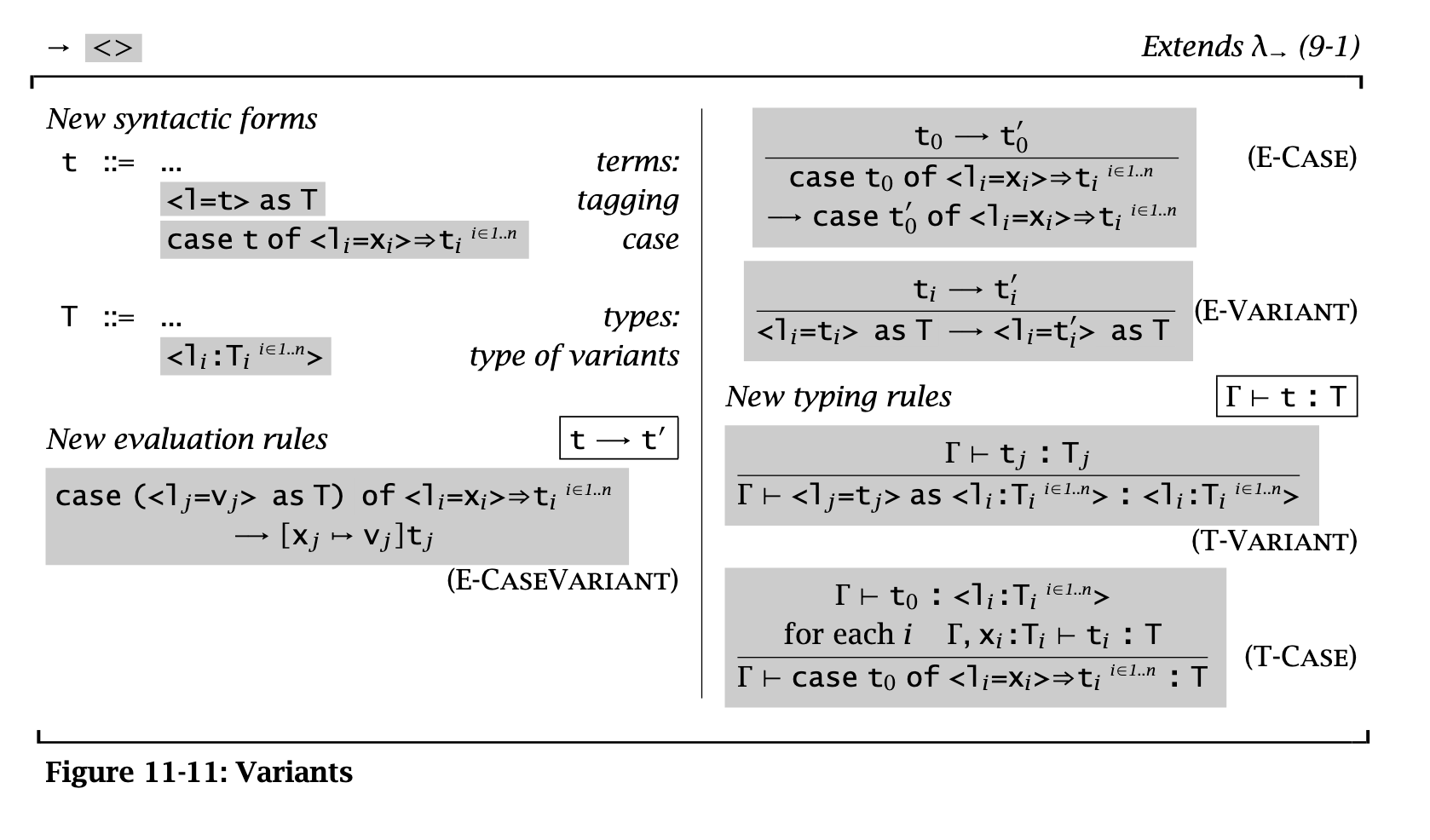
These are analogous to Haskell ADTs with some caveats (variants with one Unit arg don’t need to mention that arg, no parameterized datatypes, no recursive datatypes)

Recursion

The intuition is that the higher-order function ff passed to fix is a generator for the iseven function: if ff is applied to a function ie that approximates the desired behavior of iseven up to some number n (that is, a function that returns correct results on inputs less than or equal to n), then it returns a better approximation to iseven—a function that returns correct results for inputs up to n + 2. Applying fix to this generator returns its fixed point—a function that gives the desired behavior for all inputs n.

fix can’t be defined in STLC (and no non-terminating computation can be typed with only “simple” types). So we add it as an explicit construct: