nielsonPrinciplesProgramAnalysis1999a

Summary

In application, argument flows to parameter & abstraction body value flows to application

See also

While nominally notes for the relevant PoPA chapter, this also incorporates explanations from these lecture notes from Jonathan Aldrich, these Harvard lecture slides, and this page from Matt Might.

Who cares?

With imperative programs, we can compile down to a control-flow graph and perform dataflow analysis on these graphs. However, when examining functional programs, this isn’t so obvious:

1. There’s no clear notion of a “program point” with obvious predecessors or successors
2. Computation is intrinsically nested
3. Since functions are first-class, dispatch can be dynamic—the body of a function can transfer control to an arbitrary function passed in as an argument.

Control flow analysis is a form of program analysis, like dataflow analysis, that is more well-suited to performing analyses like constant propagation on functional languages. One property of control flow analysis is that along with recording the information we care about, we also record the possible functions every subexpression could evaluate into. This info is needed for performing analyses in the presence of first-class functions, since whenever we have a function application, we need to know what functions might be applied at that point (i.e., where control flow might be coming from or to).

This analysis is also called constraint-based analysis since it relies on the generation of constraints on analysis values for variables and expressions.

0-CFA analyses

Note

This exposition follows with both the Aldrich lecture notes and the textbook presentation. We’ll be switching back and forth where needed.

In this section, we’re going to build up to a constant propagation analysis on a functional language. We’ll get there eventually, but we’ll work up to it!

Now of course, we want to record analysis values for variables, but since functional languages rely on expressions, we also want to record analysis values for expressions as well. We do this by associating each expression with a label . Our analysis thus maps from either a variable or a label to a lattice value , which is the output type of our analysis:

Textbook difference

The textbook separates into two components: an abstract environment , which has type and abstracts over execution environments, and , which has type an abstracts over execution profiles—traces of executed expressions. Additionally, instead of , they use .

Additionally, you could get away with having an analysis just be from if you transform to continuation-passing style or A-normal form, since all expressions become “labeled” by variables. We don’t do that here to show that this sort of analysis doesn’t require a transformation into e.g., CPS to work.

is the abstract domain of the analysis.

Before we get to a full constant propagation analysis, we’re gonna do a simpler analysis that this analysis depends on: figuring out what functions an expression can call! The values a function could return (and thus what constants an expression could evaluate to) depends on the functions it is transferring control flow to, and the arguments given to those functions.

In control flow analysis, at every occurrence of a function application, we want to be able to know what functions we might be calling at that point. In other words, whenever we see , we want to know: what values could take on? We do this by associating every subexpression with a set of possible functions that the subexpression could take on. Thus, for now, our lattice type is:

So, how can we define this analysis? We define this analysis in terms of constraints over the possible analysis values for a variable or label. We then solve the constraints afterwards to get the most precise analysis value at each point.

In the Aldrich lecture notes, this analysis is given as inference rules that generate constraints. For instance, this rule states that a constant expression with label (remember—all expressions are labeled!) yields () no constraints:

Aldrich

Equivalently, the textbook defines an acceptability relation , which states that is an acceptable control flow analysis of the expression . To define our constraints, we state under what conditions this relation holds. Here is the constant acceptability relation:

Textbook

Now, let’s look at the how both treatments deal with the rule for variables. The rule broadly states that for a variable , we need to check if the analysis value for is a subset of (in lattice-land, smaller than) that of :

Aldrich

Textbook

Note that at this point, they’re specializing for the set analysis, and aren’t thinking about lattices:

Since you’ve probably gotten a flavor for translating between Aldrich and the textbook, I’ll be using the textbook’s syntax from now on, since it’s more standard I guess.

When we encounter a function, it’s pretty straight-forward: we add a constraint that our analysis should include the fact that “this expression could evaluate to this lambda term”:

Textbook

Note that this definition doesn’t demand that we analyze the body of the function at all. Instead, we do this analysis at function application, since we don’t care about unreachable expressions.

Function application is more complex. Let’s say we have an application . Our analysis needs to check a few things:

• We must have valid analyses at and .
• For every function in the analysis set for (i.e., the first expression):
  • We must have a valid analysis at the body of the function , and
  • The possible set of functions that formal parameter in the lambda could evaluate to must include the possible set of functions stood for by the argument , and
  • The set of function values this application can take on must include the values of the body of the function .

Textbook

Constraint flow rule-of-thumb

We can summarize the way that constraints flow thusly: the argument flows to the parameter, and the abstraction body flows to the application. Consider an application

• The argument flows to the parameter means that flows to . That is, the analysis for must be a subset of the analysis for . .
  • Whatever analysis that holds for the argument must also hold for the parameter, since when the function is called, the parameter takes on at least that argument as its value.
  • The parameter could take on other arguments in other places, hence why it’s argument subset parameter and not other way around.
• The body flows to the application means that flows to . The analysis for must be a subset of the analysis for .
  • Function application will eventually yield , the body of the abstraction.
  • The analysis for will take into account all the possible concrete values of the parameter.
  • Thus, the analysis for should also hold for , which provides one possible concrete value of the parameter.
  • This is an over-approximate analysis, since it assumes the analysis for , which is taken assuming that could take on all sorts of values at different application points, is a subset of the analysis for .
  • But this is the safe, conservative estimate!

In general, we can say that concrete values flow to abstract variables. Application arguments flow to formal parameters, and concrete return values or function bodies flow to the variables they’re assigned to.

Remember this rule of thumb. It will apply in general to the modifications of 0-CFA we will explore shortly.

Sensitivities and polyvariance

See also

https://en.wikipedia.org/wiki/Data-flow_analysis#Sensitivities

This analysis has a number of properties:

• It is flow-insensitive: if we have an application , even if our analysis of is empty (i.e., it can’t take on any lambda values), we still perform analysis of anyways. ^70155c
  • A flow-sensitive analysis would skip analyzing if it determines to be empty.
  • This is because call-by-value (i.e., strict) semantics insists on a left-to-right calling order, which means that a flow-sensitive analysis—an analysis that takes into account order of execution and control flow—should analyze first and use that to inform whether it should analyze .
  • By contrast, our flow-insensitive analysis ignores the semantics of our language, and analyzes both and regardless.
  • See the notes for Exercise 3.3 on page 204 of the textbook.
• It is path-insensitive: when we encounter conditionals, the analysis for each branch doesn’t depend on or incorporate information about the predicate expression of the conditional.
  • From Wikipedia: “A path-sensitive analysis computes different pieces of analysis information dependent on the predicates at conditional branch instructions. For instance, if a branch contains a condition x>0, then on the fall-through path, the analysis would assume that x<=0 and on the target of the branch it would assume that indeed x>0 holds.”
• It is context-insensitive: the analysis treats all function calls to the same function the same, regardless of where that function is being called. We’ll go over this in depth in Context sensitivity k-CFAs and m-CFAs.
  • Note that monovariance is another word for context insensitivity, and polyvariance is another term for context sensitivity.

On flow- and context-sensitivity and -insensitivity

Alias Analysis for Object-Oriented Programs provides a more detailed look at flow-sensitivity & -insensitivity and context-sensitivity & -insensitivity.

Adding dataflow information

Note

This references §3.5 of the textbook.

Now, let’s return to our constant propagation problem. We don’t want to just keep track of what expressions call what functions; we want to keep track of other information as well, like we might with a dataflow analysis!

Basically, we can just extend the abstract domain to not just contain the set of functions, but to also contain whatever other extra information we want! For example, in the textbook, §3.5.1 describes an analysis that stores both which functions are called, as well as a set of properties about the expressions: if they are a true or false bool, or if they are a negative, positive, or 0-valued integer.

So, let’s do constant propagation analysis! Remember that in constant propagation analysis, each value is either , , or an integer . We can denote this possible set of values as —the set of integers with both top and bottom. There are two different ways of treating extra dataflow information: keeping it separate from, or combining it with, control flow analysis.

In the textbook, we keep these things separate. The textbook defines a monotone structure to consist of a lattice and a set of monotone functions . Additionally, we need to be able to lift constants and binary operations on those constants into lattice values. Formally, this structure must consist of a mapping from constant in the language to a lattice value in , and a mapping from binary operation to a function in . A monotone structure for constant propagation analysis would set . In an instance of this structure, we map , and define a function that performs addition in the presence of and .

Because of this, we also introduce abstract data values , abstract data environments , and abstract data caches .

Now, statements are in the form:

where the in just means “this has dataflow stuff involved” I guess. We update our rules accordingly:

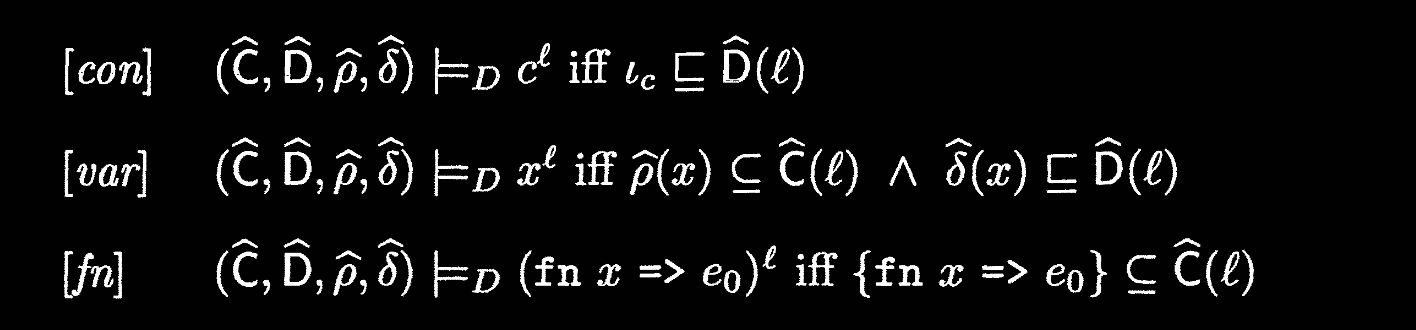
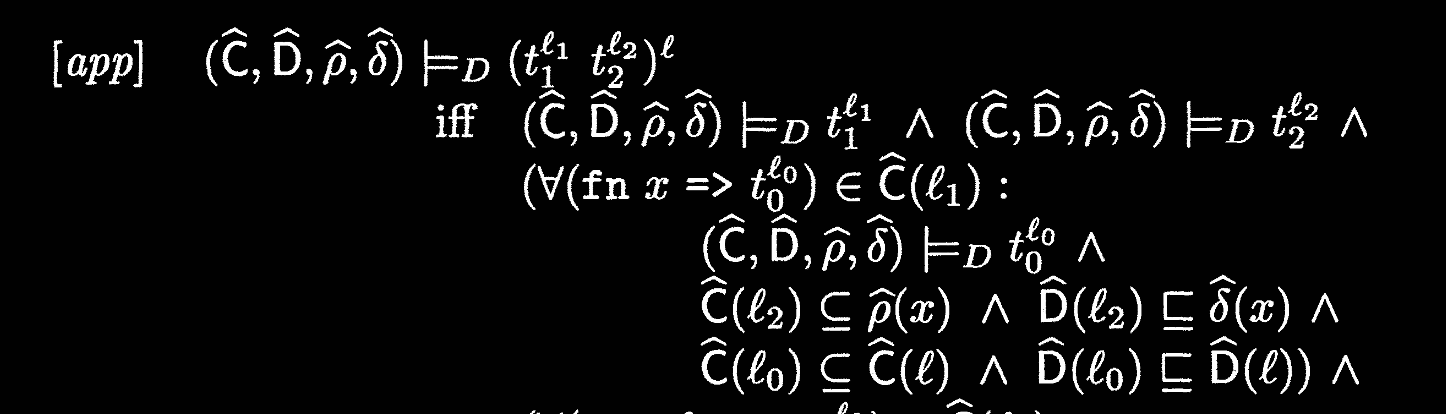
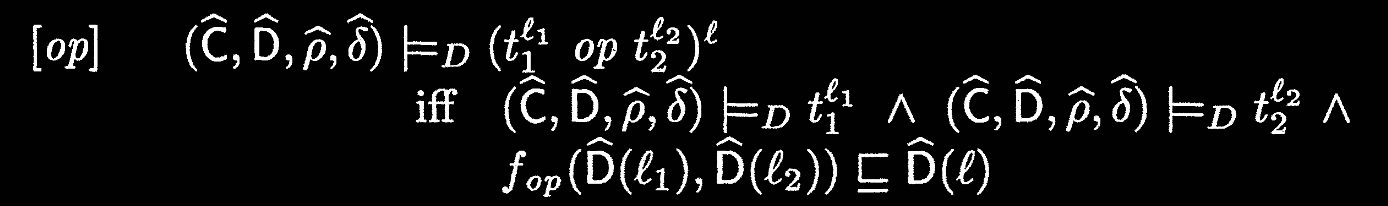
Explanations:

• For constants, the constant should be in our analysis.
• For application, we propagate following our rule-of-thumb as before: argument to parameter, lambda body to application.
• For binary operations, calling the appropriate lifted operation on the arguments should be less than the analysis for the whole expression

Alternatively, in the lecture notes, we define as the union between control flow analysis and our constant propagation analysis. This simplifies the rules somewhat:

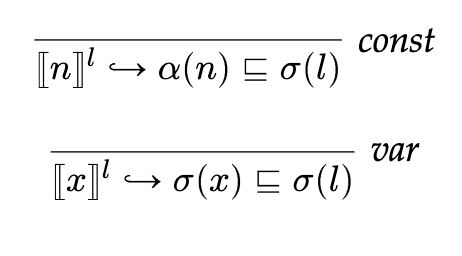
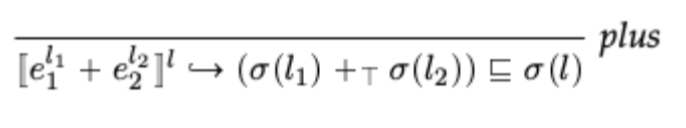
where is analogous to in the textbook’s treatment.

Context sensitivity: k-CFAs and m-CFAs

Note

This references §3.6 of the textbook.

So what do we mean by context sensitivity of analyses? Let’s look at the following expression:

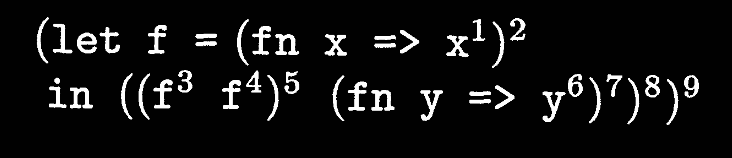
In our current analysis, we note the following:

• x in fn x => x can take on one of two values: fn x => x from (4) and fn y => y from (5).
• We return x in (5) and (8); since x can be either value, (5) and (8) must also be either value.

However, the expression ultimately evaluates to fn y => y, meaning our analysis is imprecise! It thinks the expression could have two possible values, but that’s wrong. The key error here is lack of context—the analysis can’t distinguish between f f and (f f) (fn y => y), i.e., f (fn y => y). Only the second call is actually responsible for dictating the possible function values (9) can take on!

if we explicitly divide f into two different functions, called in different places, our analysis then works:

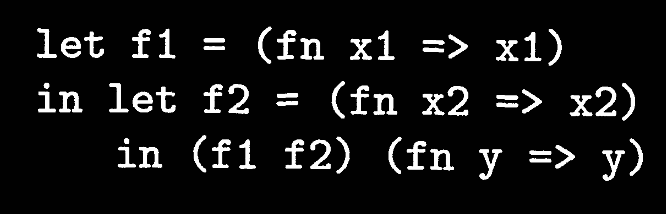
Here, the analysis proceeds as follows:

• x1 only takes on f2, and f2 only takes on fn y => y.
• By application, (f1 f2) includes the fns in the body of f1—i.e., f2.
• By application again, f2 includes only the fns in the body of f2—i.e., fn y => y

The analysis can now realize that x1 can only be bound to fn x2 => x2, and x2 can only be bound to fn y => y. Thus, when calling the overall expression, only fn y => y is a possible value.

The difference here is context. The variable f occurs in different places, but in each place, its argument x can take on different values, as was made clear when we split its uses out into two different functions f1 and f2. The difference is in the expressions that were evaluated before each call of f—basically, the call stack that led to this application of f! This is what we mean by the context and by “occurring in different places.”

In the literature, context-sensitivity is also referred to as polyvariance, with context-insensitivity referred to as monovariance.

k-CFAs

In a -CFA analysis, whenever we come across a function application, we record it in a context , which contains the last function calls. Thus, a context is a sequence of labels of length at most :

Our abstract environment now requires us to provide both a variable and the context in order to get the analysis value:

Of course, we need to now store contexts in our analysis too. Indeed, at each subexpression point, we want to store the mapping from all free variables in a term to the (up to) most recent applications before that variable was bound. Why only free variables, you might ask? We’ll get to that soon :)

We call this mapping a context environment. The context environment will determine the context associated with the current instance of a variable in a subexpression.

Our abstract value domain is now a set of tuples: the abstraction that subexpression could take on, and the local context environment at that subexpression:

Uniform -CFA analysis vs. -CFA analysis

Confusingly, a uniform -CFA analysis differs from a -CFA analysis. In the uniform -CFA analysis, our treatment of the abstract cache mirrors the abstract environment, taking a product of labels and contexts:

However, in a regular -CFA, we have . I believe these are functionally equivalent, and just differ in terms of framing? We call the former “uniform” since both the abstract environment and abstract cache use the same precision.

So how do we go about performing this analysis? First, let’s look at the notation for our acceptability judgment now:

Our judgment is now with respect to a context environment and a context . It’s helping to think of these as a sort of “global state” of the algorithm building up constraints; when analyzing subterms of , we will require that judgments with modified and —based on our current values—of the subterms hold.

Now, let’s look at function introduction:

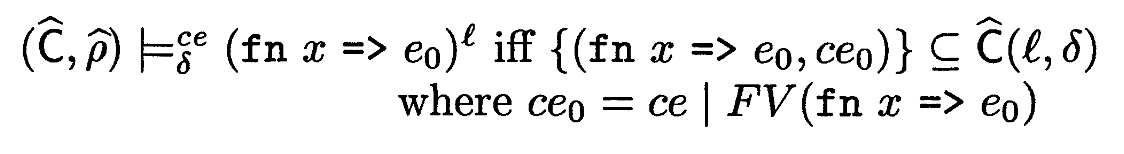
The analysis information we store at must contain the lambda itself, as before, along with this current context environment: the global context environment restricted to only map from free variables within the function. We do this because we introduce information about into at function application time! Speaking of:

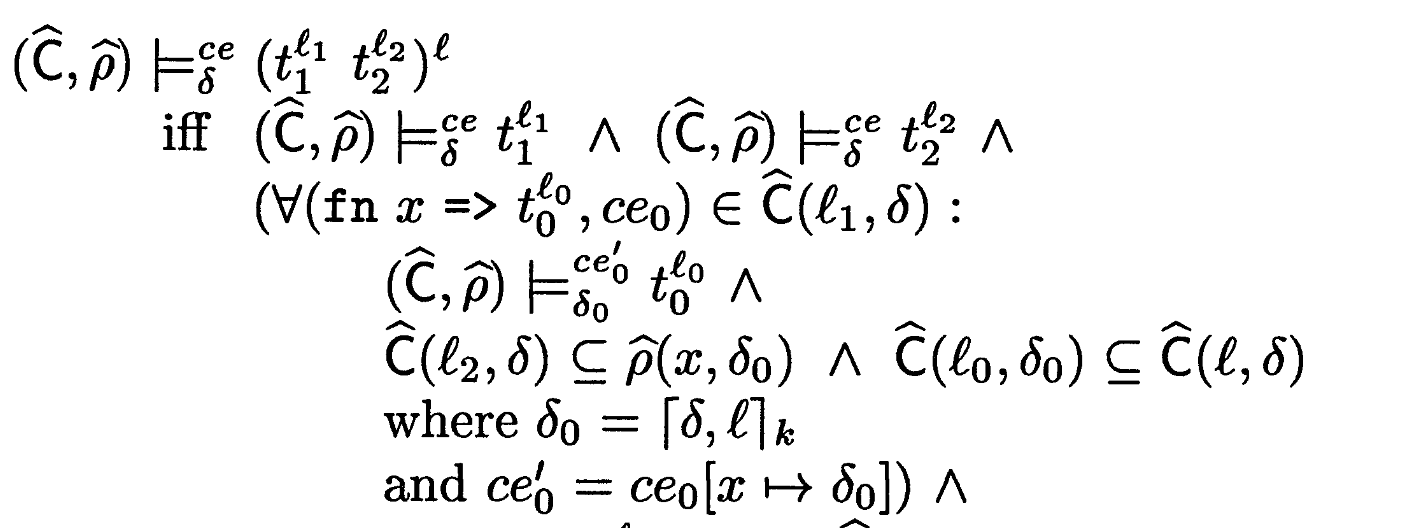
Let’s unpack this rule:

• Let’s say and are the current environment and context as we’re performing this analysis.
• Checking the body involves a new context environment and a new context .
  • now contains , the most recent application.
    • is their notation for ” with appended, then truncated to the most recent .”
  • now maps from , the newly bound variable, to the context at this point.
    • Remember that is the mapping for all free variables in the lambda.
    • isn’t free in the lambda term; thus provides a mapping for .
    • Remember that the meaning of a variable being in an environment is “whatever the call stack was up to when this variable was bound”
    • We preserve free variables because inside , is now free, and we want to retain that information as-is for .
• Remember the rule-of-thumb for how constraints propagate: argument flows to parameter, value of body flows to application:
  • Argument flows to parameter:
  • Body flows to application:
  • Be careful about threading the right arguments in the right places!

And for completeness, here are the other two rules:

A worked example

TODO

Haven’t done this yet.

Tradeoffs & space complexity

Note

Also taken from the Harvard lecture slides.

So if adding context makes our analysis better, why not do it all the time?

The summary is that -CFA has exponential space complexity, even if ! In the case, if you have a size expression with different variables, will have different elements—as expression size grows linearly, the number of labels grows linearly, and a context must be a single label, since . Thus, , a mapping from , has possible values.

Since is a powerset of pairs , and there are pairs it follows that has height . Since we have the exponential worst case complexity claimed above.

By contrast, 0-CFA analysis corresponds to letting be a singleton; there’s only one possible . is a lattice of height with respect to program size, which has polynomial complexity (as we’ll see in Practical implementation).

From k-CFA to m-CFA

Note

Now we reference the above slides and this paper.

From above, it turns out -CFA is exponential time. However, other folks have found that performing -CFA in object oriented settings is polynomial time!

The reason this is is because objects are subtly different than closures. Within a closure, each variable could be bound in a different context. This is why our has to map from ; each variable could have a different context, because closures can capture outside variables!

By contrast, in OO languages, objects can’t capture outside variables. Instead, whenever they create a “closure,” they have to call a constructor that explicitly copies the variables into the object, so they can be referenced at that point. Think of how Rust handles closures internally: it explicitly creates a struct that copies all of the variables at that point into its own state:

let x = 4;
let f = || {
  x + 1
}();

is equivalent to

struct F {
  x: u32,
}
 
impl F {
	fn call(&self) -> u32 {
		self.x + 1
	}
}
 
let x = 4;
let f = (F { x }).call();

Because of this, all variables are bound in the same context. doesn’t need to map from , since it’ll be the same regardless of what . Thus, , restoring polynomial time, since will have possible values.

This is the core idea of -CFA: instead of recording the last call sites, we record the last stack frames. Instead of keeping track of one context per variable, we record one context only: the scope in which a closure was captured (i.e., where a lambda happens I guess).

Cartesian Product Algorithm

See also

Read Cartesian Product Algorithm first!

For a language with multi-argument function calls, we can rephrase 0-CFA analysis to act on cartesian products of the arguments.

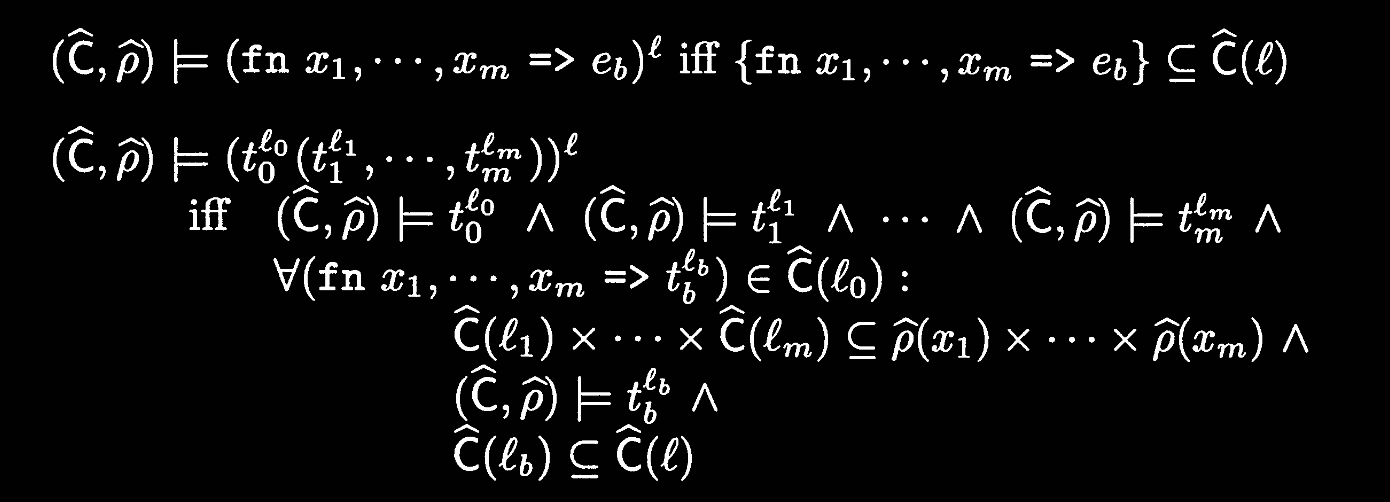
With the Cartesian Product Algorithm, we see a way of implementing context sensitivity in the presence of multi-variable functions. This is kind of implementing -CFAs, since we capture all variables at once. A context now is a product of terms. We construct a context in function application by performing a cartesian product on the sets of all possible analysis values for each argument. This product must be in the product of all possible analysis values for the output variables.

In essence, following our rule of thumb, analysis flows from products of analyses on concrete values to products of analyses on abstract variables.

Practical implementation

Note

This references §3.3-3.4 of the textbook.

Okay. That was a lot of theory. In this section, we’re gonna cover how might we implement CFA constraint generation and solving in practice.

The goal is to find the smallest solution , where “small” is given by the partial order on the product lattice of :

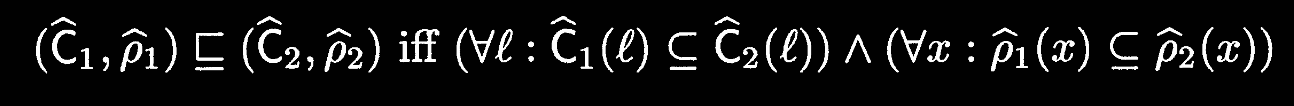
Our approach will be to reformulate the specification of into one that’s more suited for computation:

1. We’ll change the spec in a syntax-directed manner
2. We use this new spec to define an algorithm for generating constraints
3. We’ll compute the least solution of this set of constraints.

Syntax-directed specification

Our syntax-directed reformulation ensures that every function body is analyzed at most once. We do this by moving body analysis into lambda introduction—instead of where it was in application, i.e., lambda elimination. This has the cost of analyzing potentially unreachable program fragments (e.g., analyzing the body of a function that’s never called).

Syntax-directed constraint generation

With this new spec, we can define a syntax-directed constraint generation algorithm!

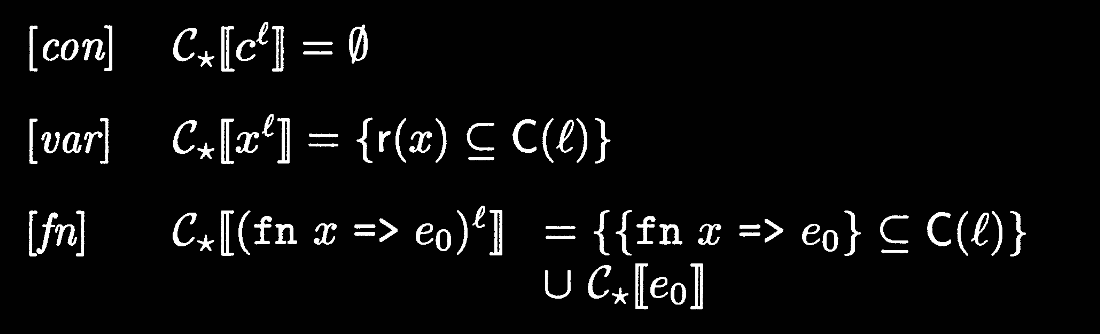
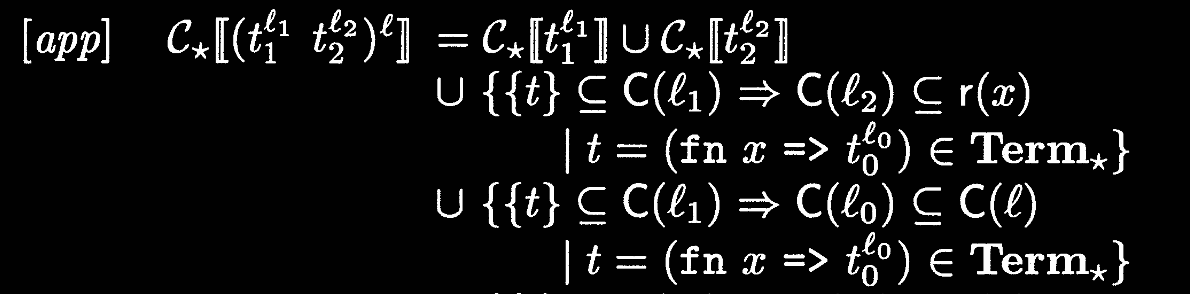
Notation notes

• We read as .
• What does it mean to have an implication be a subset of another set? The next section will clarify this!

Solving these constraints

How do we solve these constraints? There are two broad solutions:

• Fixed-point, complexity over size of the expression .
  • On each iteration, we update the abstract cache as follows:
    • For every label in the environment
    • Get every constraint of the form .
    • will have one of two forms. We must transform into a set of terms:
      • If is a set , return .
      • If is , this means .
      • If is of the form :
        • If , transform .
        • Otherwise, return .
        • When we say “transform,” we mean “do the same pattern matching we just did on .”
      • Remember that we have to do this because we have that “implication subset” notation going on above.
    • Combine all transformed items to yield .
  • Do the same with the abstract environment.
• Graph reachability****, complexity . ^203nd2
  • The nodes are all the variables and labels. Each node contains the analysis, initially initialized to every term mentioned in a constraint.
  • A constraint creates an edge
    • This edge is traversed only whenever has a new term.
  • A constraint creates edges , .
    • These edges are only traversed if is in the analysis for .

Either of these algorithms produce the least solution to , and thus the least that satisfies .

We can’t really check if an abstract environment and cache are acceptable for an expression though. This is important when we’re trying to optimize and not ; maybe the latter represents assumptions about our environment, meaning we can swap out and any optimizations based on a choice of will continue to hold so long as .