§ 20. Recursive types
Often when defining types, we want types to be able to refer to themselves. Consider the canonical linked list in Haskell:
data List a = Nil | Cons a (List a)It refers to itself! These are recursive types. In the textbook, they use an explicit recursion operator µ for types, so a NatList would be defined as follows:
NatList = µX. <nil:Unit, cons:{Nat,X}>;
where X basically represents Self. The definition is read: “Let NatList be the infinite type satisfying the equation X = <nil:Unit, cons:{Nat,X}>.”
Uses
An infinite list can be defined as the following type:
Stream = µA. Unit -> {Nat,A};
Constructing elements of this type can be done with the fix operator:
upfrom0 = fix (λf: Nat→Stream. λn:Nat. λ_:Unit. {n,f (succ n)}) 0;
We can generalize this as a Process that takes in number states as messages:
Process = µA. Nat -> {Nat, A}
Getting the current state of the process and sending new states to the process is defined as follows:
curr = λs:Process. (s 0).1;
send = λn:Nat. λs:Process. (s n).2;
We can represent objects in a purely functional way like this! Think Self type:
Counter = µS. {get:Nat, inc:Unit->S};
Definition is done through fix:
c = let create = fix (λf: {x:Nat}→Counter. λs: {x:Nat}.
{get = s.x,
inc = λ_:Unit. f {x=succ(s.x)},
dec = λ_:Unit. f {x=pred(s.x)} })
in create {x=0};
The auxiliary definition create is responsible for setting state.
Well-typed fix
fixT = λf:T→T. (λx:(μA.A→T). f (x x)) (λx:(μA.A→T). f (x x));
The domain of x must be x itself. We can satisfy that here!
But with recursion, any expression can diverge:
fixT (λx:T. x)
Typing rules: iso-recursive vs equi-recursive
There are two possible approaches to recursive types. Each of these differs in how they treat a type µX.T and its one-step unfolding. For instance, what’s the relationship between NatList and <nil:Unit, cons:{Nat,NatList}>?
The equi-recursive approach treats these two things as definitionally equal. The only different that’s required is that we need to allow type expressions to be infinite, and we can’t do induction on type expressions.
The iso-recursive approach sees these types as different but isomorphic. In this approach, we must introduce new constructs that let us “witness this isomorphism” and translate between isomorphic types:
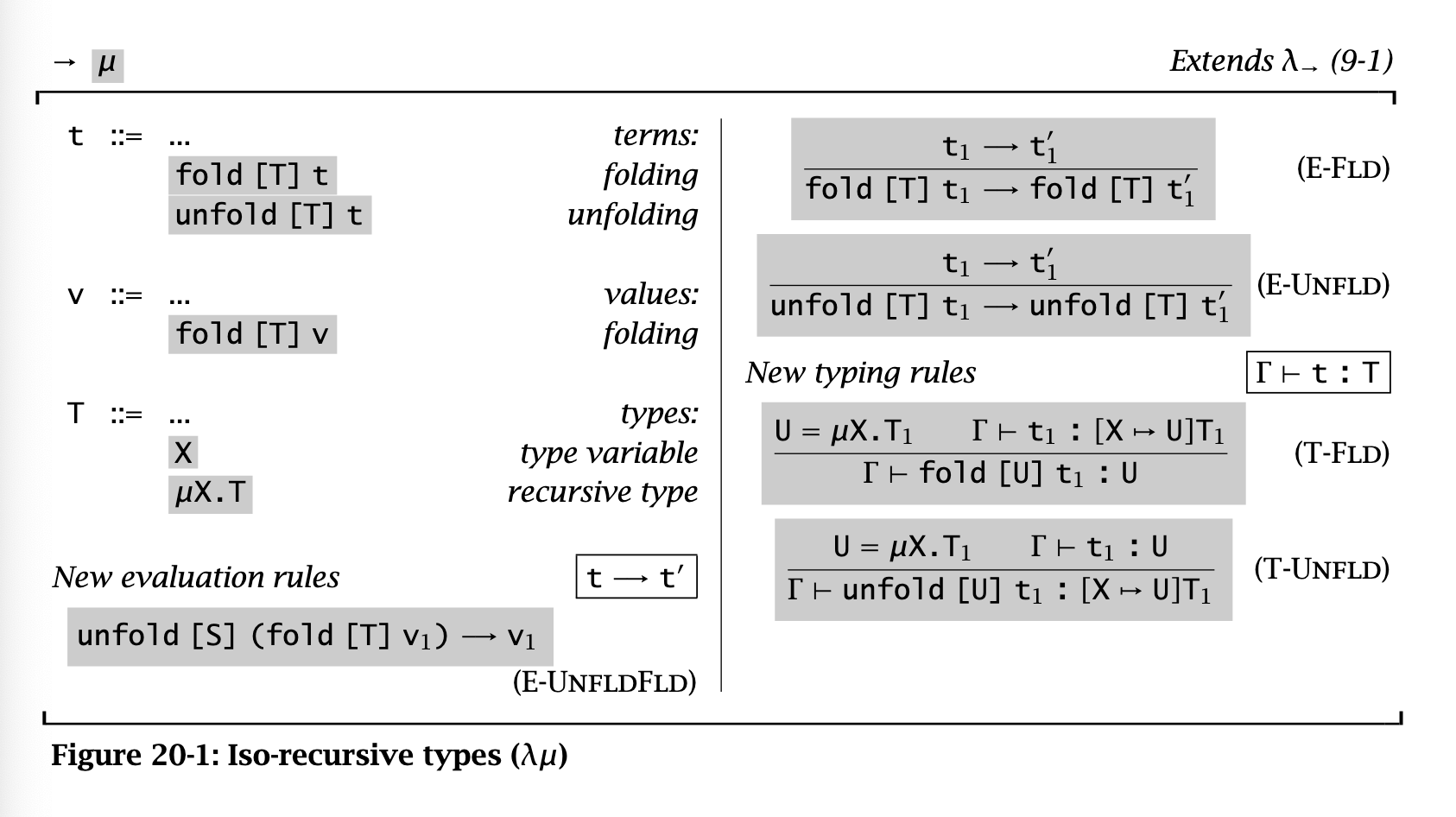
Here, the unfold operator goes one level deeper of replacement, while the fold operator undoes this substitution.
The equi-recursive approach is notationally lighter, but much harder to implement, since you basically have to infer fold/unfold annotations. Plus, interactions with other advanced features like bounded quantification and type operators can be complex and maybe undecidable.
The iso-recursive approach is the one most often used in practice; here, the annotations are “hidden” by making them be added automatically. For instance, in ML languages, a datatype definition implicitly introduces a recursive type. Constructors introduce a fold, while constructors in pattern matches introduce an unfold.
§ 22. Type reconstruction
We’re starting to talk about polymorphism! Let’s fucking go. In this chapter, we talk about type reconstruction: which can infer a principal type for each term.
Type variables and substitutions
In this calculus, our uninterpreted base types are type variables that can be substituted or instantiated with other types. Type substitution consists of creating a type substitution
Views on type-checking type variables.
Let’s say
- Is
well-typed for all possible type substitutions?
- Is
well-typed for some possible type substitution?
If we’re trying to look at question 1, then type variables should be held abstract during type-checking, which ensures that a well-typed term will behave properly no matter what types are substituted in at the end. This is parametric polymorphism, i.e., generics!
In the circumstance of question 2, the term
λf:Y. λa:X. f (f a);
Treating Y and X as uninterpreted base types, this isn’t well-typed as is, but if we can substitute in X -> X for Y, we can get:
λf:X→X. λa:X. f (f a);
Which is valid!
Trying to find any valid substitution of type variables is type reconstruction, i.e., type inference. Given a context
Constraint-based typing
This is an algorithm that, given a term
For instance, if we see
A constraint set
The typing rules for the constraint typing relation
Here, the subscript is just the empty set, since this judgment doesn’t introduce any new type variables.
The general intuition is that, given
Here are all the type rules:

CT-Var,CT-Zero,CT-True, andCT-Falseare straightforward.- Function calls that would have enforced the type of their arguments (
CT-Succ,CT-Pred,CT-IsZero) instead add a new constraint that whatever type the argument is, it should be aNatorBool. CT-Ifcombines all of the constraints for the predicate and bodies, introducing new constraints that ensure that the predicate is aBooland the bodies have the same type. Here we see the importance of having the subscript, since it allows us to make sure that there’s no weird variable shadowing happening between constraints across different branches. - Finally,
CT-Appis the only rule that introduces a new type variable. Since there’s no existing type that refers to the result of the application—could be itself just a type variable, after all, this rule gives a brand new type variable to the result of the application, enforcing the constraint that is a function from the argument type of to our new variable . All of the noise ensures that and are totally disjoint and don’t mention any free variables in either of the type expressions, and that the new type variable isn’t mentioned anywhere. - In practice, we would have a function that generates fresh type variables.
TODO
There’s a progress and preservation proof here. Induction on type judgments, etc.
Unification
When you hear a “Hindley-Milner” type system, this is where that comes from: they came up with using unification to find the “best” solution. The best solution is the most “general” solution.
Let’s formalize what we mean by that. A substitution
In other words, the most general solution is the minimal substitution required to satisfy a constraint set, the substitution from which all other substitutions can (and must!) be built on.
Here’s the algorithm!
data TypeExpr = Var String | Arrow TypeExpr TypeExpr
data Constraint = Eq TypeExpr TypeExpr
data Subst = String :-> TypeExpr
compose :: [Subst] -> [Subst] -> [Subst]
notFreeIn :: String -> TypeExpr -> Bool
-- [Constraint] should be Set Constraint but I want pattern matching syntax!
unify :: [Constraint] -> Maybe [Subst]
-- If there are no constraints, the empty substitution satisfies
unify [] = Just []
unify ((Eq s t):cs) = case (s, t) of
-- If the equation is already satisfied, don't need to add substitutions
(s, t) | s == t <- unify cs
-- If the equation is in the form X = blah, X must map to blah in our subst
(Var x, t) | notFreeIn x t <- fmap (`comp` [x :-> t]) $ unify cs
-- If the equation is in the form fuck = X, X must map to fuck in our subst
(s, Var x) | notFreeIn x s <- fmap (`comp` [x :-> s]) $ unify cs
-- If we have two arrow types, the parts before the arrows
-- and the parts after should be equal
(Arrow s1 s2, Arrow t1 t2) <- unify $ cs ++ [Eq s1 t1, Eq s2 t2]
-- else, fail
otherwise <- NothingThe notFreeIn is an occur check, which prevents generating a cyclic substitution like X :-> X -> X, which we don’t want (unless we allow recursive types).
This algorithm will always terminate, either failing if the constraint set is non-unifiable or returning the principal unifier for the expression.
Principal types
A principal solution for
If we have principal types, we can build a type inference algorithm that’s more incremental. Instead of generating all constraints and then solving them all, we can return a principal type at each step instead. Since these types are always principal, we never need to re-analyze a subterm.
Implicit type annotations
With this machinery, we can now introduce the inferred-type lambda abstraction construct, typed as follows:
This introduces a new type variable
Let-polymorphism
Polymorphism means language mechanisms that allow reusing a single part of a program with different types in different contexts. Let-polymorphism is a simple form of this, introduced with ML (it’s also called ML-style polymorphism for this reason). The motivating example is as follows:
let double = λf:X->X. λa:X. f(f(a)) in
let a = double (λx:Nat. succ (succ x)) 1 in
let b = double (λx:Bool. x) false in ...
In the expression for a, double is inferred to have type (Nat -> Nat) -> Nat -> Nat, which means it can no longer be used with b. Parametric polymorphism (i.e., generics) is the full answer here, but let-polymorphism is a simple modification that gets us part of the way there.
At a high level, the signature of double is telling us about the relationship between the types of the arguments of this function, but as of right now, our type system also enforces a relationship between the types of the arguments of double across different calls of the function. This is because the double.
So how can we do this? Well, from the last section, we have a mechanism for introducing fresh type variables whenever an abstraction is defined. But with our let binding type rule, we concretize a specific type for a let-bound variable (and thus a specific choice of type variable in double) when type-checking:
Instead, we can substitute
Type-checking let definitions
Now, this formulation has some issues. First, since we no longer type-check let-bound variable definitions, we can pass in something like let x = bullshit in 5 and it’ll still type-check, which we don’t want. So we can add a premise to the let rule that ensures
Note that this is still different than the original let rule, since we’re not including
Efficiency improvements
Another problem is that the let-bound variable definition is now type-checked on every occurrence of the variable—since we’re substituting it directly into the expression—which can cause exponential blow-up since the right-hand side can itself contain let bindings. To avoid, this, languages use a different reformulation of these rules that’s more efficient:
- Use constraint typing to find type
and constraint set for . - Use unification to find the principal type
of . - Generalize the remaining type variables in
. is no longer a type, but a type scheme, representing the structure of a type with respect to universally quantified holes.
- Extend the context to record this type scheme for the bound variable
, and type-check . - Whenever
occurs in , generate fresh type variables and use them to instantiate the type scheme for , yielding , which becomes the type of in that use.
This is mostly linear, but can still exhibit exponential blowup if lets are nested in the right-hand sides of other lets.
See also
For more on doing constraint-based type checking and inference with generics-style polymorphism, see Instantiation and generalization.
Side effects
Finally, side effects can fuck this up. For example:
let r = ref (λx. x) in
r := (λx:Nat. succ x);
(!r) true
In line 1, r is inferred to have type scheme r to
This is caused by a mismatch in types and semantics. In our typing rules, we basically create two copies of the ref, each of which is typed differently. But in our semantics, only one ref is ever allocated. In our typing rules, we immediately substitute the definition in the body, while in our semantics, we only do substitution after the let-bound var definition has been reduced to a value.
One way of fixing this is adjusting evaluation to immediately substitute:
Under this evaluation system, our example works, but doesn’t do what we would expect:
(ref (λx. x)) := (λx:Nat. succ x) in
(!(ref (λx. x))) true;
These lines no longer refer to the same ref, but instead create a brand new one every time.
The other option is to adjust typing, imposing the restriction that a let-binding can be treated polymorphically only if its right-hand side is a syntactic value. This is called the value restriction, and in practice it doesn’t actually result in a significant reduction in flexibility.
Notes
The biggest success story in this arena is the elegant account of type reconstruction for record types proposed by Wand (1987) and further developed by Wand (1988, 1989b), Remy (1989, 1990; 1992a, 1992b, 1998), and many others. The idea is to introduce a new kind of variable, called a row variable, that ranges not over types but over entire “rows” of field labels and associated types. A simple form of equational unification is used solve constraint sets involving row variables. See Exercise 22.5.6. Garrigue (1994) and others have developed related methods for variant types. These techniques have been extended to general notions of type classes (Kaes, 1988; Wadler and Blott, 1989), constraint types (Odersky, Sulzmann, and Wehr, 1999), and qualified types (Jones, 1994b,a), which form the basis of Haskell’s system of type classes (Hall et al., 1996; Hudak et al., 1992; Thompson, 1999); similar ideas appear in Mercury (Somogyi, Henderson, and Conway, 1996) and Clean (Plasmeijer, 1998).
§ 23. Universal types
We looked at let-polymorphism before. Now, let’s look at a more general form of polymorphism, in a more powerful calculus: System F. It’s Haskell time!!!!!!
Types of polymorphism
Before we get into this, let’s describe what polymorphism means. There are many kinds of polymorphism:
- Parametric polymorphism: basically, generics. Instantiate type variables per use as needed.
- Impredicative polymorphism (i.e., first-class polymorphism) is the most powerful form of this
- Let-polymorphism (i.e., ML-style polymorphism) restricts polymorphism to top-level
letbindings and disallows functions that take polymorphic values as arguments, in exchange for better type inference.
- Ad-hoc polymorphism: …
- Subtype polymorphism: …
System F
System F introduces a few concepts to our lambda calculus:
- Universal quantification. At the type level, we explicitly introduce type variables as their own construct and not just an uninterpreted base type. We can also write types that do universal quantification over these type variables:
- Type abstraction and application: there is a new term
which introduces a fresh type variable that can be referred to in a term. Accordingly, there is a new application form . - Type annotations are part of the term language, so we need to do this
- As an example,
id = λX. λx:X. x;
- Contexts contain type variable bindings. Now, a context can also contain a list of type variables, to ensure uniqueness etc.
The semantics and typing rules for System F are shown below:

Well-typed System F terms are normalizing (progress & preservation).
Erasure, typability, and type reconstruction
A term m in untyped LC is typable if there is some well-typed term t such that erase(t) = m. The type reconstruction problem asks: given an untyped term m, can we find a well-typed term that erases to m. Type inference!
For System F, this is undecidable. Even if you only erase what type is applied in type application terms, it’s still undecidable. There are a few strategies for recovering some inference abilities:
- Local type inference
- Greedy type inference: any type annotation can be skipped, replacing with a type variable. We do subtype checking until we see either
or , at which point we set . This is simplest, but maybe not best. Lots of spooky action at a distance. - Let-polymorphism
- This is a special case of System F where type variables range over quantifier-free types (monotypes) and quantified types (polytypes, i.e., type schemes) can only appear on the right side of arrows
- Rank-2 polymorphism: a type is rank-2 if no path from its root to a
quantifier passes to the left of arrows. is rank-2 is not.
Erasure & evaluation order
Right now, we have a type-passing semantics; when a polymorphic function meets a type argument, we substitute that type into the function body. This is a runtime evaluation thing.
Instead, we can have a type-erasure semantics, where types are first erased before untyped terms are interpreted or compiled.
There are some things we have to keep in mind with this semantics. For instance, erasing types from this expression:
let f = (λX. error) in 0;
and turning it into this:
let f = error in 0;
changes the semantics of the function. Thus, we just need to make sure deferred evaluation because of type lambdas is preserved in the erased form.
Parametricity
A parametric type can restrict the definition of a function! id’s definition is kinda self-evident since there’s only one thing you can do with an a: return it!
Impredicativity
A definition (of a set or type) is impredicative if it involves a quantifier whose domain includes the thing being defined. For instance, in the type
§ 24. Existential types
We’ve seen
We write existential types as
- The logical intuition that an inhabitant element of this type is a value of type
for some unknown - The operational intuition that an inhabitant element of this type is a pair
{*S, t}of a typeSand a termtof type.
We can interpret {*S, t} as a package or a module with a hidden representation type S (i.e., a witness type), and a term t. Since from the type of this value, we only know that there exists some representation type
For example, if we have:
p = {*Nat, {a = 5, f = λx:Nat. succ(x)}}
This can be type
Here’s the full new rules for adding existential types to System F:

T-Unpack is interesting since when unpacking an existential type, it hides the specific implementation type used for packing. The type of the term x is given in terms of an abstract bound existential X, not a specific type like X is used to syntactically introduce the type variable, not to bind to the actual value of the type.
Additionally,
Data abstraction with existentials
Let’s talk about abstract data types (ADTs). With ADTs, we can only interact with them using the operations defined on the ADT. Its concrete representation is made opaque to outside interactors. Here’s a counter ADT:
ADT counter =
type Counter
representation Nat
signature
new : Counter,
get : Counter -> Nat,
inc : Counter -> Counter;
operations
new = 1,
get = λi:Nat. i,
inc = λi:Nat. succ(i)
We can translate this into existentials:
counterADT =
{*{x:Nat},
{new = {x = 1},
get = λi:{x:Nat}. i.x,
inc = λi:{x:Nat}. {x = succ(i.x)}}}
as
{exists Counter, new:Counter, get:Counter -> Nat, inc:Counter -> Counter}
Objects
To get objects, our ADT should have the following structure:
ADT = {exists X, {state:X, methods:{...}}}