winskelWinskelDenotationalSemantics1993

IMP: a simple imperative language

Before we begin, we need to define a simple imperative language used by the book, termed IMP. This language features assignment of numerical expressions to mutable reference locations.

Imp’s syntax:

a = n | X | a0 + a1 | a0 - a1 | a0 * a1  (* math expr, num lit, or location *)
b = true | false | a0 = a1 | a0 <= a1    (* booleans *)
  | not(b) | b0 and b1 | b0 or b1 sd 
c = skip | X := a | c0; c1 | if b        (* statements *)

c is “commands”

Who cares about denotational semantics

• It can handle a bunch of PLs (though not parallelism and “fairness”)
• We can compare what different PLs can do; if they can represent similar programs
• We want to directly define what commands are equivalent.

A denotational semantics for IMP

In the operational semantics for IMP, the single-step evaluation relation on arithmetic exprs (a/Aexp) (exprs of metavar c) is defined as a function that takes a command and a state and returns a natural number. The relation on booleans returns a Bool, and the relation on commands returns a new state, where a state maps from locations to the natural numbers. It’s our reference state, basically. stands for the set of all possible states .

In this setting, let the denotation (i.e., meaning) of an arithmetic expression be a function that takes a state and returns a natural number: . Alternatively, you could think of as a function of type , taking in some expression in our language and returning a function that corresponds to that expression’s meaning

Similarly, a boolean expression denotes a function , and a command denotes a function .

On the brackets

Denotational semantics girlies love their double brackets . This is to denote that the expression inside the double brackets shouldn’t be evaluated—essentially a kind of quasiquoting that can also contain metavariables!

To actually define these functions, we do induction.

Notice that we define partial functions via set/relation on pairs syntax. means that . Boolean expressions are fairly straightforward too.

For commands , it’s slightly more complicated. The first few steps are pretty straightforward:

Composition is a little funky. Let’s say we have two statements , where maps from state and maps from . This set of statements as a whole should map , which we get by composing .

For if statements, the function depends on if the boolean is true or not:

For while loops, things get a little dicey. For a while expression , this is the same as (a recursive definition)! Thus, we can define while’s denotation in terms of if, giving us an equation for the denotational semantics of :

This gives us an equation that we can solve to figure out what 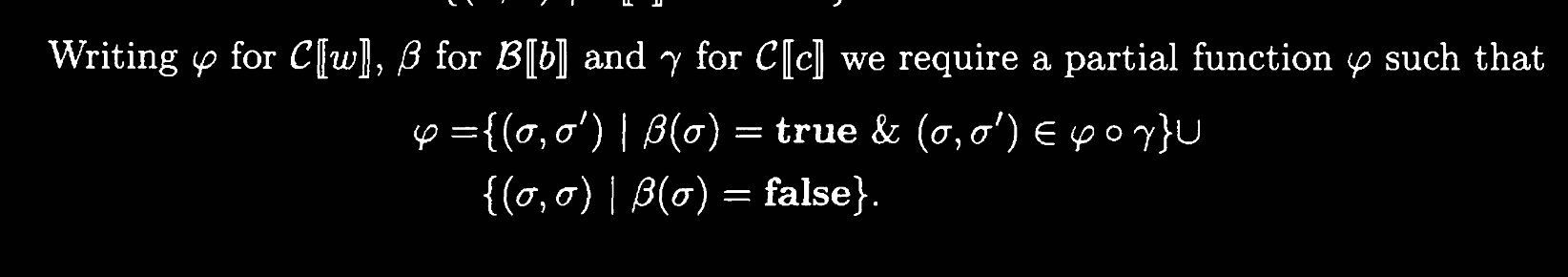should be. To clean this up slightly, the book substitutes , and :

With this, we can then define a function 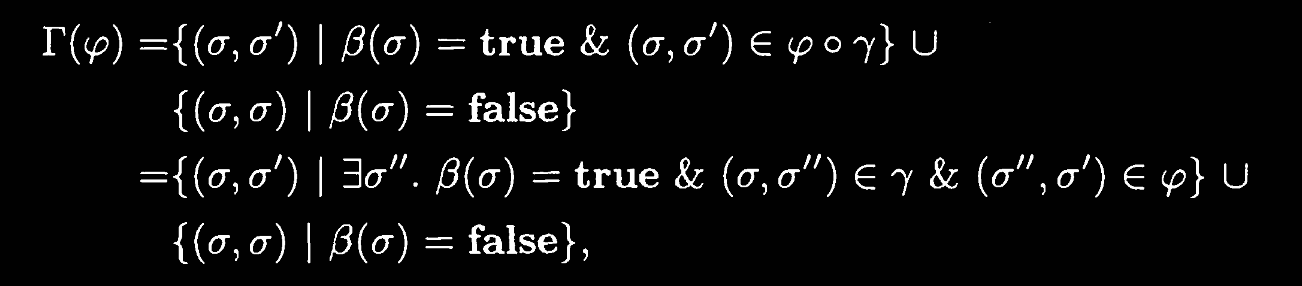that takes a value (corresponding to while loop iterations) as its input, and returns the value of at iteration as its output:

So now we no longer have recursion, but generating “layers” or “stages” of whiles. is iter 0, is iter 1, is iter 2, etc. So we just define .

Proving this is equivalent with operational semantics

For and , it’s sufficient to do induction on the expression. For , we show through rule induction on operational semantics of commands, and we show the reverse direction through structural induction on commands.

Complete partial orders and continuous functions

From this point on, notes are moved to denotational semantics and domain theory since I need to synthesize hella different documents to figure out what’s going on lmao