§ 6. The axiomatic semantics of IMP
Other reading
There are a lot of connections with Introduction to Program Verification 9/6 9/11. Look at that too!
Axiomatic semantics is fitted for proving that a program written in a language does what we require of it. It’s called axiomatic semantics since we are explaining the meaning of programs by stating rules saying how to prove properties of the construct. To create a formal proof system for proving properties of programs, we’re gonna use Hoare rules! Let’s fucking go!!
Just as an overview, since we touched on Hoare rules (i.e., Hoare triples) in ^9a4f4c. A Hoare rule for partial correctness
Additionally, we say
On bottom
As convention, we can write
if it is undefined. We can also adopt the convention that , we can describe the meaning of as:
To explain this, we go through an example of defining axiomatic semantics for IMP.
Formally defining assertions and Hoare rules
For the assertion language for IMP programs, we extend boolean expressions Bexp with universal and existential quantifiers. We also extend arithmetic expressions with arbitrary (free) integer variables; this class is called Aexpv by the literature.
Interpreting these expressions now requires both a state
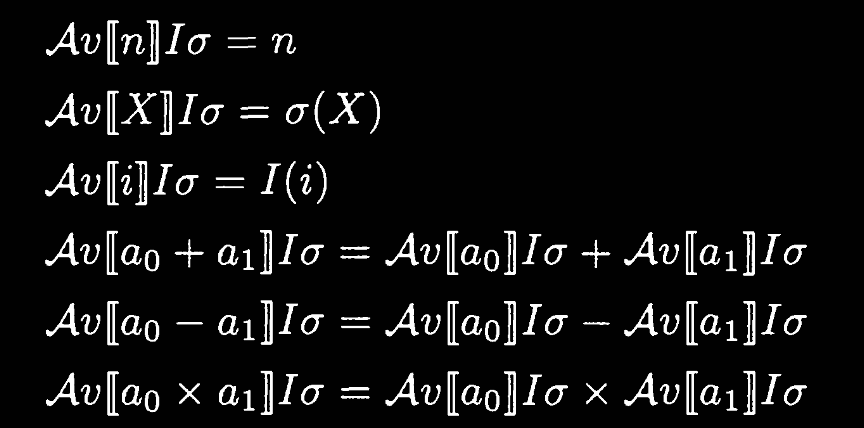
This is a denotational semantics.
Notation for substitutions
Their syntax for substitutions is
, which should be read .
The meaning of assertions
This is a more axiomatic definition, where we directly define those states which satisfy an assertion. We define the operation

The extension of an assertion
Partial correctness
Now, we can define a Hoare rule
with respect to some interpretation
Validity
We define the following operation:
This means that the Hoare rule holds for all states and interpretations. In general,
Axiomatic semantics
When we define axiomatic semantics for commands, we present them in the form of inference rules, since axiomatic semantics are meant to help us prove properties about programs!

These are the same rules as discussed in Introduction to Program Verification 9/6 9/11; specifically ^8a9qz6.
versus Since these are rules, there’s a notion of derivation for Hoare rules. Derivations are proofs, and any conclusion of a derivation is a theorem. We write
when it is a theorem.
Properties
There are two properties we care about for such a logical system:
- Soundness: if the assumptions in the rule’s premise are valid, so is its conclusion.
- Completeness: all valid partial correctness assertions should be able to be obtained as derived theorems.
§ 7. Completeness of Hoare rules
See also
This overlaps with discussion of weakest preconditions from the CS 264 notes.
Gödel’s Incompleteness Theorem states that there’s no proof system for partial correctness assertions where all theorems are mechanically provable (i.e., effective). For instance,
However, the system from above is still complete; if a partial correctness assertion is valid, there exists a proof of it with Hoare rules.
Weakest preconditions and expressiveness
Again, see the relevant discussion in CS 264 notes for more info.
In this book, the weakest precondition is defined as the set of states where execution of
Assn is expressive iff for every command
More notation: the assertion expressing a weakest precondition is defined as:
for all interpretations
TODO
There’s a proof of Assn’s expressiveness and relative completeness that follows. I’ve skipped it here.
Verification conditions
See the CS 264 notes for more.
Verification conditions are a way of mechanically generating weak-ish preconditions for verifying program correctness.
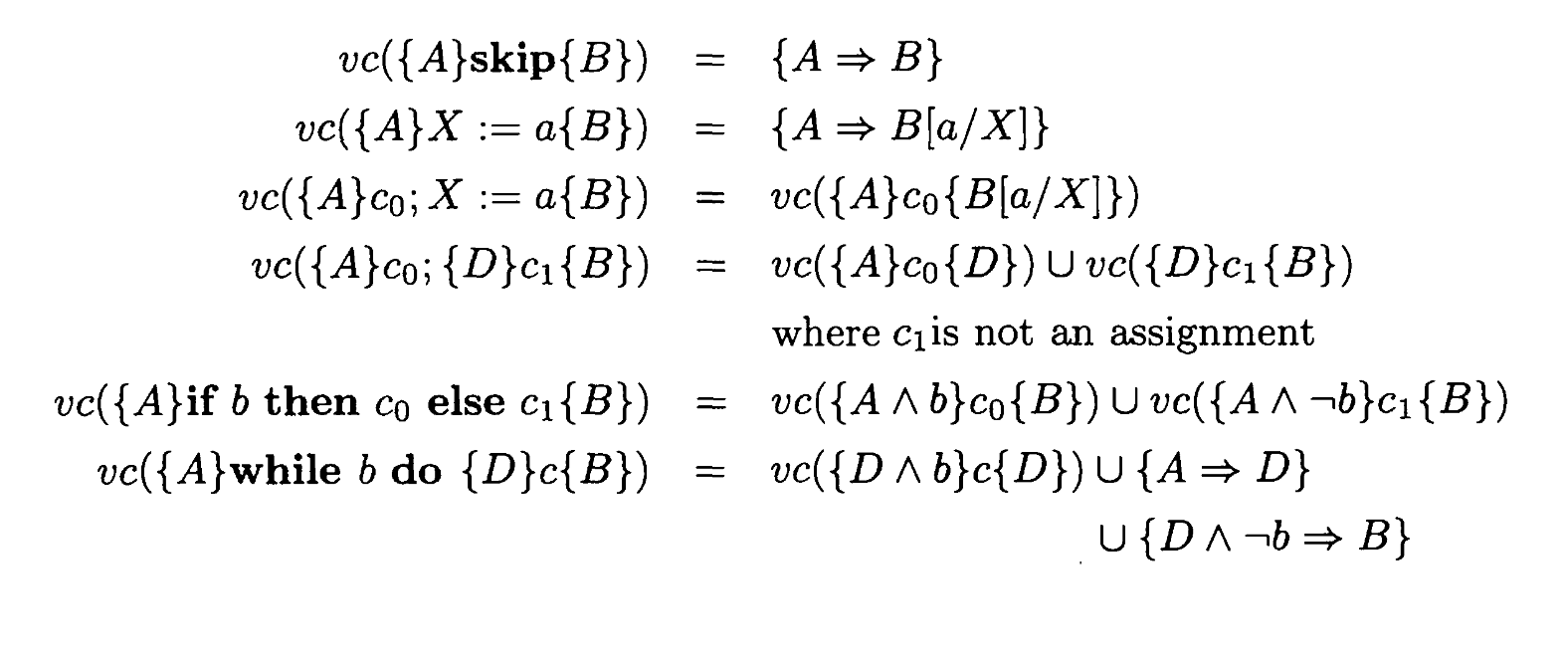
The result of the function vc is a set of assertions about the properties of the program.
TODO
I’ve also skipped the section on Predicate transformers; I have no idea what those are.
§ 8. Introduction to domain theory
See denotational semantics and domain theory, since we need to synthesize multiple sources for this one.