david's pl notes

ahoDragonBookMachineindependent2007

Sep 02, 202432 min read

Summary

If backwards, ,

Kinds of analyses: Reaching: what definitions are relevant at program point? Availability: Has an expression as defined at this point been used before? Is it available for use? Liveness: Will an expression as defined at this point be used again later? Is it still alive and will be used later? Constant propagation: Each var is , , or a constant value

Optimizations: Constant folding: constant propagation Common subexpression elimination, code motion: partial redundancy elimination Dead-code elimination: liveness Copy propagation

Let’s discuss basic opportunities for global optimization!

Most global optimizations rely on data-flow analyses—algorithms that gather info about a program. These analyses all specify some property that must hold every time some instruction in a program is executed. The analyses differ in what they compute. For example:

  • Constant-propagation: does a variable contain a unique constant value at some point?
  • Liveness analysis: at this point in the program, will a variable’s value be overwritten before it is read again?

The principal sources of optimization

Using high-level languages often introduces redundant operations. For example, if you do array access via A[i][j], you’re doing pointer arithmetic under the hood, which might end up being duplicated. In this section, we provide some examples of semantics-preserving transformations/optimizations.

  • Global common subexpressions: if an expression was previously computed and the values of the variables in haven’t changed since the previous computation.
  • Copy propagation: If we have a copy statement x = v somewhere, wherever we use x afterwards, we should use v instead. This might not seem to change anything, but this helps improve dead-code elimination. Speaking of!
  • Dead-code elimination: if a statement computes values that are never used, it can just be removed. This is why copy propagation is important; if we have x = v; y = 2 * x, with copy propagation + dead-code elim we can remove x entirely!
  • Constant folding: deducing at compile time that an expression’s value is constant and using that constant value
  • Code motion: If an expression in a loop yields the same result on every iteration, it’s taken out of the loop ^9d6c9d
    • e.g., while (i <= x - 2) becomes t = x - 2; while (i <= t)
  • Induction variables & strength reduction: if a variable changes by a constant c on each reassignment, it’s an induction variable. Strength reduction is replacing an expensive op (e.g., multiplication) with a cheaper one (e.g., addition).

Intro to dataflow analysis

Dataflow analysis refers to techniques that derive info about flow of data along execution paths. For example, dead code analysis is “do any execution paths use this assignment?” Global common subexpression elimination is “do two textually identical expressions evaluate to the same value along all execution paths?”

The dataflow abstraction

A program is a series of transformations on program state—values of variables. The input state of a statement is associated with the program point before a statement, while the output state is associated with the program point after a statement.

An execution path is a sequence of points such that:

  1. immediately precedes a statement and immediately follows that statement, or
  2. is at the end of some block and is the beginning of a successor block.

In dataflow analysis, we don’t distinguish between paths taken to reach a program point, and we don’t keep track of entire states, just what we need for an analysis. For example:

  1. To help users with debugging, we might want to know all the values a variable might take on at a program point, and where those values were defined. Maybe a variable a is one of and was defined at either statements or . The definitions that may reach a program point along some path are reaching definitions.
  2. If a variable x is reached by only one definition (i.e., x only ever refers to one definition), and the definition is a constant, we can replace x with the constant. However, if several definitions reach x, we can’t do this constant folding. We only do constant folding if there is a unique reaching definition for the variable, and it assigns a constant. When doing analysis, we only record const-ness, not necessarily all possible values or definitions.

The dataflow analysis schema

Every program point has a dataflow value, an abstraction of the set of all program states that can be observed for that point. The set of possible dataflow values is the domain.

For example, for reaching definitions, we care about recording subsets of definitions; statements where definitions occur. This would be the dataflow value for a program point, and the domain is the set of all subsets of definitions.

The dataflow value before and after a statement is denoted with and . The dataflow problem is to find a solution to a set of constraints on ‘s and ‘s, for all statements in the program.

There are two sets of constraints.

Transfer functions

Transfer functions are constraints on dataflow values based on the semantics of statements themselves. For example, if a has value before executing b = a, after executing this statement, both a and b will have value . The relationship between dataflow values before and after statements is called a transfer function.

Information can propagate in one of two directions:

  • Forward-flow problem: the transfer function operates on the pre-state, returning to the post-state:
  • Backward-flow problem: the transfer function converts a dataflow value after the statement to a new one before the statement:

Control-flow constraints

Control-flow constraints on dataflow values are derived from the flow of control. For instance, within a basic block, since statements just execute one after another, we know that the control-flow value out of some statement must be the same as the value into the following statement :

Between basic blocks, since basic blocks might have multiple predecessors, often we will do union operations or things like that, e.g.,

Dataflow schemas on basic blocks

Since the goings-on within basic blocks are pretty simple, we can define the above operations on basic blocks as a whole:

  • , and
    • This is useful for writing control flow constraints between basic blocks.
    • We write the constraints acting on basic blocks, then rewrite them to reference statements.
  • Transfer functions can operate on basic blocks.
    • In forward direction: , where
    • or in backward direction: , where

These equations normally don’t have a unique solution. But we want to find the most “precise” solution.

What can we use dataflow analyses for

A lot!

Reaching definitions

Where might a variable x have been defined at program point ? A definition reaches point if there is a path from point immediately after to , such that isn’t killed on this path. A definition is killed if there is any other definition of x along that path. A definition is any statement that may assign a value to x.

We want to perform an analysis that records which definitions—of any variable—are relevant (i.e., reaching) at a particular program point. So for instance:

d1: x = 1       // {d1}
d2: y = 2       // {d1, d2}
d3: z = 4       // {d1, d2, d3}
d4: x = 2       // {d2, d3, d4} since x has been killed.

So how might we write the equations for this? First, let’s look at the transfer equations. Let’s look at a definition:

d0: u = v + w

This statement “generates” a definition of u and “kills” all other definitions of the program that define u, whether before or after this point. Remember that the dataflow value of each program point is the set of definitions that are live at a program point, for all variables. After this statement is executed, should be added to the dataflow value, while all other definitions that define u should be killed. We encode this intuition as follows:

where is the set of definitions generated by this statement—in this case, —while is the set of definitions killed by this statement—any prior definition that defines u.

Note

The concept of and sets occurs a lot in other contexts:

Why do we do all other definitions that define u, and not just definitions before? To be conservative, we assume that all edges of a flow graph can be traversed, even if this isn’t necessarily the case, as in the following program:

if (a == b) mayRun();
else if (a == b) neverRuns();

We can generalize these operations to blocks as well:

Basically, is all definitions killed in the basic block, and are all definitions generated in the basic block that are not killed by subsequent statements in that same basic block. A definition in is also referred to as downwards exposed.

Note that in a basic block, a variable can be in both the kill and gen set. If it appears in both, its gen-ness takes precedent, since set difference on the kill set is applied first. For instance:

           // gen  kill
d1: a = 3  // {d1} {d2} -- we kill all other definitions, forward or back!
d2: a = 4  // {d2} {d1}
 
           // basic block
           // gen: {d1} cup ({d2} - {d2}) = {d1}
           // kill: {d2} cup {d1}         = {d1, d2}

For our control-flow equations, we do:

If a basic block has two predecessors, the definitions of both basic blocks may reach this one. Union is called the meet operator in dataflow schemas, which is the operator used to create a summary of contributions from different paths at the confluence of those paths.

Thus, the summary of our equations is as follows:

We can find a solution to this with an iterative algorithm that just repeatedly calculates and for each basic block (in that order), repeating until least fixpoint.

Least fixpoint

When we say least fixpoint, we mean that this fixpoint is contained in all other fixpoints.

Liveness analysis

See also

https://en.wikipedia.org/wiki/Live-variable_analysis

An example of a backward-flow dataflow problem. In liveness analysis—specifically, live variable analysis—we want to know: given a variable x and a program point , does the value of x at get used later on in the program? If so, it is live at . Otherwise, it’s dead.

Here, instead of asking, “what definitions of x are potentially used at ,” we’re asking, “does the definition of x at get used in the future?” The former question is asking about previous definitions, and so is a forward-flow. The latter asks about future uses, and so is a backward-flow. If a variable is used at some point in the program, we want to propagate this information backwards, so that earlier program points know that later in the program, the value is used, and thus the variable is lived.

This is useful for e.g., register allocation. If a value is computed in a register within a block, we don’t need to keep it there if it’s dead at the end of the block.

Let’s look at the following basic block as an example:

a = f(b * c)
b = 3
c = 4

At the point before the basic block, since a, b, and c were re-defined, we want them removed from the live variables list. However, we want to add b and c, since they were used before their redefinition in the block. With respect to the point before the block, they are used again in the basic block before getting redefined, meaning that at that point, they are live!

We include b and c into the gen set, since they’ve been used before they’ve been defined in this basic block. We want these variables to be added to our analysis value, since them being used before a definition means that at the start of the basic block, they are live.

However, a, b, and c are all in the kill set, since they’re all defined within this basic block. When propagating backwards, we want to remove everything in the kill set—removing everything that has been defined in this basic block—but then add everything in the gen set—adding everything where the use is before the definition, meaning the variable is live before this basic block, since we know for sure it is used within the basic block but before a re-definition.

We encode this intuition as follows:

  • is the set of variables used in before any assignment in that basic block.
  • is the set of variables defined in .

we also include the base case , and the control flow equation:

In the algorithm, we calculate before .

Available expressions

This is used for global common subexpression detection. An expression x + y is available at point if it doesn’t need to be recomputed at ; i.e., every path from the entry node to evaluates x + y, and there are no subsequent assignments to x or y between the last occurrence of the expression and .

The intuition is: “at , has x + y been evaluated as-is before?”

Confusingly, this also uses “generating” and “killing,” but with different definitions to the above. An expression is generated if it is used in a statement, and it is killed whenever a variable it references is redefined. This is a forward-flow problem.

For our control flow equation, the meet operation is intersection instead of union, because we want expressions that are available in all branches (“every path”); if it’s not available in one branch, that means it can’t be shared with other branches, and so isn’t available.

In sum:

Since we do intersection, our initial assumption is that , where is everything.

Dataflow formally

We’re gonna back up and discuss a broader theoretical framework for dataflow analysis. This framework will allow us to answer the following questions for different dataflow problems:

  1. Under what circumstances is the iterative algorithm used for dataflow analysis correct?
  2. How precise is this solution?
  3. Will the algorithm converge?
  4. What’s the meaning of the solution to the equations?

A dataflow analysis framework consists of:

  1. A direction of the dataflow , either forwards or backwards.
  2. A semilattice, which includes a domain of values and a meet operator
  3. A family of transfer functions from to . This must include functions that can handle the boundary conditions—constant transfer functions for ENTRY and EXIT.

Semilattices

See also

egglog!

A semilattice is a set and a binary meet operator with three properties:

  1. Idempotency:
  2. Commutativity:
  3. Associativity:

A semilattice has a top element and a bottom element .

Partial orders

For more on partial orders, see denotational semantics and domain theory.

A semilattice forms a partial order, where the partial ordering operation is defined as:

Note

Another way of phrasing this:

Because of how we’ve defined top and bottom, this means that bottom is the “least” element— and top is the “most” element—.

A greatest lower bound of a set of elements is an element such that and .

Relationship with lubs

We talk about lubs in the notes linked above. What’s the relationship between glbs and lubs?

In semilattices as we’ve discussed here, the meet operation returns the greatest lower bound. Since only if , by reflexivity, and by definition. There is also a join operation, which returns the lub between two elements. A full lattice contains both a meet and join operation. Here, we present meet semilattices.

The height of a lattice is the largest number of relations in any ascending chain (a chain where elements don’t equal) in the poset.

Lattice diagrams

We can draw diagrams of lattices, pointing from top to bottom:

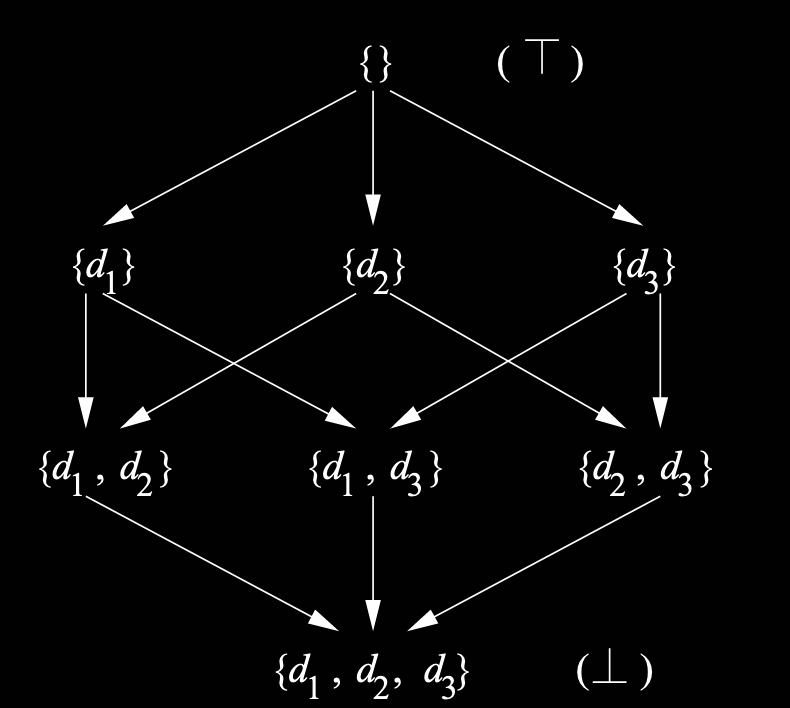
This is the semilattice for sets with union as meet.

Product lattices

  • The domain of a product lattice is .
  • The meet is .
  • The partial ordering op is

With definitions, we can regard the total lattice as a product of lattices with two elements: and .

Transfer functions

The family of transfer functions must satisfy the following properties:

  • has an identity function .
  • is closed under composition. .

Additionally, a framework can have a few properties depending on the transfer function :

  • The framework is monotone if is monotone.
    • .
  • The framework is distributive if is distributive.

Iterative algorithm

Forward:

OUT[entry] = initial value;
for (each basic block B other than entry) {
	OUT[B] = top
}

while (changes to any OUT occur) {
	for (each basic block B other than entry) {
		IN[B] = meet(OUT[P] if P a predecessor of B)
		OUT[B] = f(IN[B])
	}
}

Backward:

IN[exit] = initial value;
for (each basic block B other than entry) {
	IN[B] = top
}

while (changes to any OUT occur) {
	for (each basic block B other than entry) {
		OUT[B] = meet(OUT[S] if S a successor of B)
		IN[B] = f(OUT[B])
	}
}

This algorithm has a few properties:

  1. If this converges, it’s a solution to the dataflow equations
  2. If the framework is monotone, this is the maximum fixedpoint.
    1. A maximum fixedpoint is a solution with the property that in any other solution, the values of and are the corresponding values of the MFP.
  3. If the semilattice of the framework is monotone and of nite height, then the algorithm is guaranteed to converge.

What does this mean?

What does the solution mean from a program semantics standpoint? To explore this, let’s considering the entry of a basic block . What does the dataflow value mean at this point? Let’s consider three different possible solutions:

  • In the ideal solution, we would find the meet between all possible paths from the entry to , where possible means there is some computation of the program that follows that path.
    • Any answer smaller is a conservative safe estimate.
    • Any answer greater than this ideal solution is incorrect.
  • Finding the above is undecidable. In the meet-over-paths (MOP) solution, we find the meet between all paths from the entry to . ^6a3dc5
    • This doesn’t have a direct algorithm, since “all paths” is unbounded in the presence of cycles
  • The maximum fixpoint (MFP) solution is what we get from our algorithm
    • Compared to MOP, MFP is eager, immediately applies meet on confluence, instead of waiting to find all paths.
    • If the framework is distributive,
    • Otherwise,
    • This is because in , we visit basic blocks in arbitrary order. Additionally, we apply the meet operator to dataflow values obtained so far, including ones introduced artificially during initialization.

Constant propagation

Let’s walk through a worked example of dataflow analysis: constant propagation. This dataflow framework, unlike the previous frameworks discussed, has two interesting properties:

  1. It has an unbounded set of possible dataflow values, even for a fixed flow graph.
  2. It is not distributive.

Dataflow values

The set of dataflow values is a product lattice, with one component for each variable in a program. The lattice for a single variable consists of the following:

  • All constants of correct variable type
  • : not-a-constant. If a variable doesn’t have a constant value, it’s assigned to this.
  • : undefined. The variable hasn’t been assigned a value yet.

With these values, we can define the meet operation as follows:

This means that and .

Transfer functions & monotonicity

Let , where and are dataflow values. has the following properties:

  • If isn’t an assignment, is identity.
  • If the RHS is of the form , then
    • if and are consts
    • if either are
    • otherwise
  • Function calls or pointer assignments or whatever else are .

This captures the intuition of constant propagation. If the operands have constant values, we can compute the constant values. If they don’t, we have to give up. If any of the values are undefined, this is also undefined. Notice that takes precedence over . We only assign if we’re sure about that.

This is monotone. We can show that .

But it’s not distributive! Consider the following example:

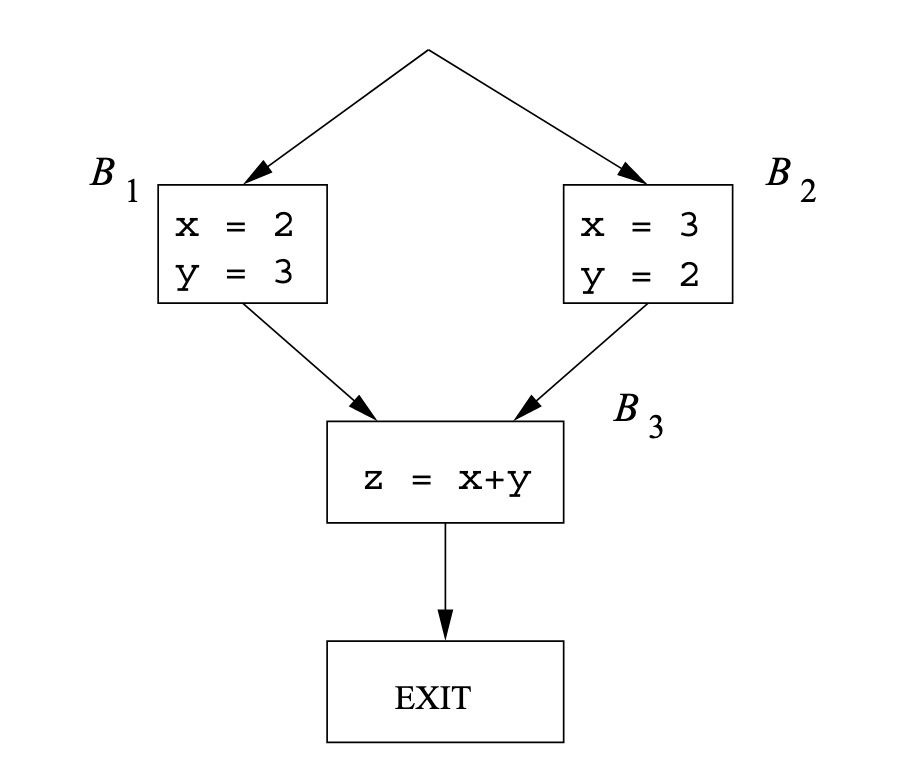
We know that in , z can be known to have value 5. But at the start of the block, in the iterative algorithm, we try to do the meet between x = 2 and x = 3, and similarly between y = 3 and y = 2. This results in z being .

Formally, let be the transfer function at block . If this were distributive, we would expect . In our example, the right hand side yields z = 5, but the left hand side yields z = NAC, so we’re nondistributive.

Partial-redundancy elimination

If an expression x + y gets used throughout our flow graph, can we reduce the number of times it’s uniquely evaluated? This covers common subexpressions, and loop invariant code motion, and partial-redundancy elimination.

We can’t eliminate all redundant computations unless we can change the flow graph by creating new blocks. Our redundancy-elimination techniques should be able to introduce new blocks, but don’t duplicate parts of the control flow graph, since the number of paths is exponential in the number of conditional branches in the program.

The lazy-code-motion problem

We want programs optimized with partial-redundancy-elim to have the following properties:

  • Redundant expressions are eliminated
  • No extra computation not in original program
  • Expressions computed at latest possible time—important for not using more register space than is needed!

The last point is what makes this lazy.

We define two kinds of redundancy:

  • An expr in a block is fully redundant if, along all paths reaching , has been evaluated and its operands haven’t been subsequently redefined.
    • Let be the set of blocks containing that renders in redundant.
    • The edges leaving the blocks in forms a cutset which, when removed, disconnects from entry.
    • No operands of are redefined along paths from blocks of to .
  • If is partially redundant, our algorithm introduces new copies of the expressions to make it fully redundant.

What's a cutset again

If we partition a graph into two sets of nodes , a cutset is the set of edges where one endpoint is in and the other is in .

Anticipation of expressions

We only want to place copies of expressions at program points where the expression is anticipated (i.e., very busy): if all paths leading from that point eventually compute with the values of and available at that point. If there exists a execution path from this point that doesn’t use , it’s not anticipated at this point.

Anticipation is the backwards analog to availability. Availability asks: “from all paths from start to here, is x + y used, and used with current x and y?” Anticipation asks: “from here to the end, is x + y with current x and y always computed?”

We do this to avoid spurious computation of an expression where it isn’t used.

The lazy-code-motion algorithm

Our algorithm has four steps:

  1. Find all expressions anticipated at each program point with backwards dataflow.
  2. Place copies of expressions as early as possible. We place them where they are anticipated—used as-is along every path going forward—but not available—if it’s anticipated along all paths before reaching that point. This is a different definition for availability than what we described above!!
  3. Postpone expressions where possible—if it’s anticipated but hasn’t been used along any path reaching the program point.
  4. Eliminate assignments to temporary variables that are only used once, using backward dataflow.

Let’s first describe the intuition for these parts.

Preprocessing

We assume every statement has its own basic block, and we only introduce new computations at the beginnings of basic blocks. If a destination of an edge has more than one predecessor, we insert a new block between the source and destination of that edge.

Anticipated expressions

For each expression, we find where that expression is anticipated—if that expression with its present value is used along all paths going forward from this program point.

When we say “anticipated or available at a block,” we mean “anticipated or available on entry to the block.”

The expression isn’t anticipated in since c is redefined in ; the value of b + c at the start of isn’t used after . b + c isn’t anticipated in since it’s unnecessary once c is redefined in , which execution may go through. Same for ; b + c might never be used again if we go straight to .

The transfer function is as follows:

Where is all expressions referenced in this block, and is all expressions whose operands were defined in this block. Meet is set intersection (“all” paths), and since this is backwards, we define:

Available expressions

Our algorithm also relies on what expressions are (not) available at each program point. Again, by available, we mean “is anticipated in all paths before this program point.” Specifically, an expression is available on exit if:

  • It’s either
    • available on entry, or
    • In the set of anticipated expressions on entry—it could be made available if it was computed here
  • and not killed in the block—none of its operands are defined in this block.

Formally, we note this in the transfer function:

Meet here is set intersection as well—all paths. With this forward analysis, we can define the set of expressions that should be placed at block : the set of anticipated expressions that are not yet available:

In this case, and

Postponable expressions

An expression is postponable to if an early placement of is encountered along every path from entry to , and there isn’t any use of after the last placement.

For instance, we can postpone to , since there’s no use of the expression after . But we can’t postpone it to , since there’s a use at ; doing this would cause a double-computation if we follow the path . We also can’t postpone the expression from to , since it’s used at .

We add expressions that we’ve seen were in , but remove them once they appear in . This is a forward analysis:

Meet is set intersection again. It’s only postponable at this block if it’s postponable at all previous blocks.

An expression is placed at the frontier where an expression goes from being postponable to not being postponable. The expressions where this is true for a block is given by . can be placed at the start of only if it’s in ‘s earliest or postponable set upon entry.

Note

Remember that postponable isn’t always a superset of earliest! For instance, for b + c, is earliest, but not postponable, since it also uses b + c.

Additionally, is in the postponement frontier of if one of the following holds:

  • isn’t in — is in . This means we should place the expression before the use in this block.
  • can’t be postponed to one of its successors; there exists a successor of such that isn’t in the earliest or postponable set upon entry to that successor.

For our example, the latest placements of b + c are and :

  • b + c is in postponable of but not because it’s used there.
  • ’s earliest set includes b + c, and it uses b + c.

Used expressions

Finally, we do a backward pass to see if any temporary variables are used beyond the block they’re in. We’re doing liveness analysis for expressions basically—an expression is used at point if there’s a path from that uses the expression before it’s reevaluated. This is backwards analysis.

Since an expression is defined at if it’s in , our backwards analysis includes expressions that are used in this block, but removes them if they’re defined in this block—are in :

This meet is union.

Putting it all together.

For every expression in the program, do the following:

  • Create a new temporary for .
  • For all blocks where , add t = x + y at the start of .
    • means it’s definable in this block, means it’s live and used later on.
  • For all blocks where , replace x + y with t.
    • The expression is mentioned, and it’s either not where an expression is defined, or it’s where a variable is live.

Dealing with loops

We need some new terminology and concepts to deal with loops in our CFGs.

Dominators

A node dominates node , written , if every path from entry to goes through . We can build a dominator tree, where the entry node is the root, and each node immediately dominates only its descendants. Every node has a unique immediate dominator that is the last dominator of on any path from entry to . In other words:

We can find dominators with a forward dataflow problem:

Dominators
DomainThe power set of , all nodes
DirectionForwards
Transfer function
Boundary
Meet
Equations

| | Initialization | |

Note that by this definition, a node dominates itself.

Additionally, we have a notion of a dominance frontier:

Additionally, we say that if there’s an edge , and a node that strictly dominates (i.e., does not strictly dominate itself) but not , then is in the dominance frontier of .

Link to original

Depth-first ordering

A depth-first search of a CFG visits all the nodes in the graph once, starting at the entry node and visiting the nodes as far away from entry as quickly as possible. This route forms a depth-first spanning tree (DFST), where a node is a child of node if is visited through .

A preorder traversal visits a node before its children, left-to-right. A postorder traversal visits a node’s children, left-to-right, before visiting itself.

A depth-first ordering is the reverse of a postorder traversal: visit a node, then its children right-to-left.

The algorithm for building a depth-first ordering and a DFST is as follows:

c = total number of nodes

search(n):
	mark n visited
	for successor s in n:
		if s is unvisited:
			add edge n -> s to DFST
			search(s)
			
	dfn[n] = c
	c = c - 1

search(entry)

where dfn[n] gives the index of the node in a depth-first ordering.

Edges

An edge of a CFG can be categorized based on the relationship of the nodes in a DFST:

  • An advancing edge is where is a proper descendant of in the DFST. All the edges in the DFST are advancing.
  • A retreating edge is where is an ancestor of . In these cases, .
  • A cross edge is where neither are true. If we draw a DFST in the order children are added to the tree left-to-right, cross edges travel right to left.

A back edge is an edge where dominates . Every back edge is retreating, but not every retreating edge is a back edge. A graph is reducible if all its retreating edges are back edges. Alternatively, a graph is reducible if no matter the DFST, the set of retreating edges is the same, and equals the set of back edges.

For an example of a non-reducible CFG:

Here, depending on how we build the DFST, we could get different retreating edges. With the DFST 1 -> 2 -> 3, the edge 3 -> 2 in the CFG is a retreating (but not back) edge. With the DFST 1 -> 3 -> 2, the edge 2 -> 3 in the CFG is that edge.

Depth of a flow graph

The depth of a graph with respect to a DFST is the largest number of retreating edges on any cycle-free path.

Natural loops

A natural loop is a loop that is well-suited for easy optimization. It has two properties:

  1. It must have a single-entry node, called the header. This dominates all nodes in the loop.
  2. There must be a back edge that enters the loop header.

Given a back edge natural loop of the edge is plus the set of nodes that can reach without going through . is the header of the loop. To find the nodes in the natural loop from a back edge, do a depth-first search on reverse control-flow graph starting with , adding all nodes visited to the loop. We mark as visited so search doesn’t go beyond there.

With this, we can identify distinct loops. If two loops have the same header, we consider them the same loop.

Speed of convergence of iterative data-flow algorithms

The maximum number of iterations the algorithm may take is the product of the height of the lattice and the number of nodes in the flow graph (for each node, we can move one step lower towards ). However, for many analyses, we can order the evaluation so that this converges way quicker.

The key thing that determines this: ==will all events of significance to a node be propagated to that node along some acyclic path, after one pass?==

  • Yes with reaching. If a definition reaches , there’s some path from block containing to where is in all analyses on this path.
  • Yes with availability. If isn’t available, there’s an acylic path where either is never generated, or is killed but isn’t generated.
  • Yes with liveness. If is live on exit from , there’s some acyclic path from to where isn’t defined.

But not with constant propagation!

L: a = b
   b = c
   c = 1
   goto L

Here, it takes three loops to get a constant value for a.

In general, we want to modify our algorithm such that for forward flow problems, we move in depth-first order, while for backward problems, we move in reverse order. In this way, the number of passes needed to propagate any definition along any acyclic path is no more than the depth plus two. This is because we can propagate all needed info forward as long as an edge isn’t retreating; if it’s retreating, we have to repropagate back down the depth order. We need at least one pass to propagate information, hence the first plus one, and we need an extra pass to check that nothing has changed, hence the second plus one.

Graph View

Backlinks