Warning
For more on model checking, see https://ptolemy.berkeley.edu/projects/chess/eecs149/lectures/Reachability.pdf Maybe look at this at some point and take more detailed notes if you want to dive more into model checking!
- Temporal logic model checking: express specs for finite-state concurrent systems in temporal logic, with circuit/protocol as state-transition system.
: true in the present if is always true.
Binary decision diagrams
Ordered binary decision diagrams (OBDDs) represent boolean formulas.
We can start with binary decision trees:
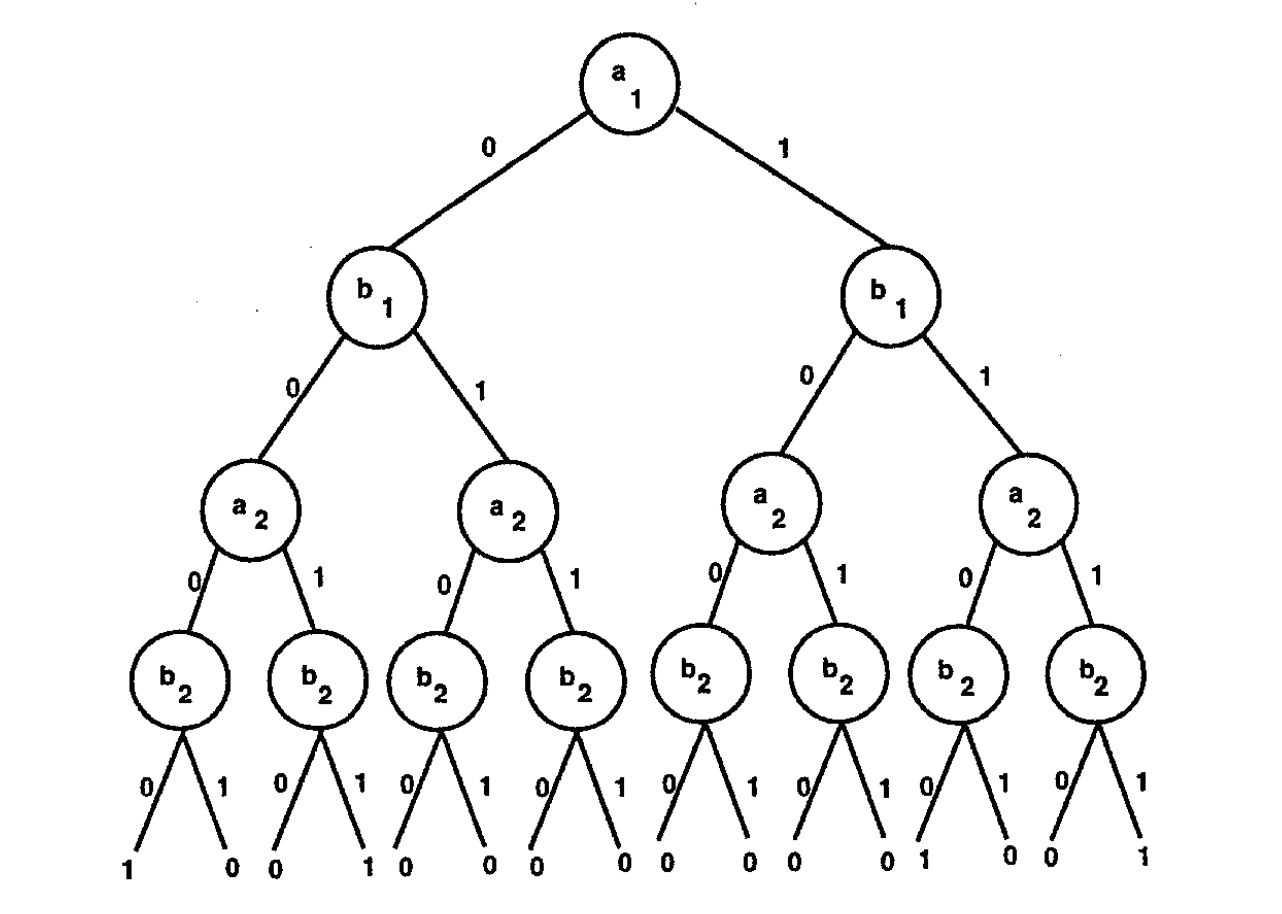
To make this way more compact, we can turn this into a binary decision diagram: a DAG basically!
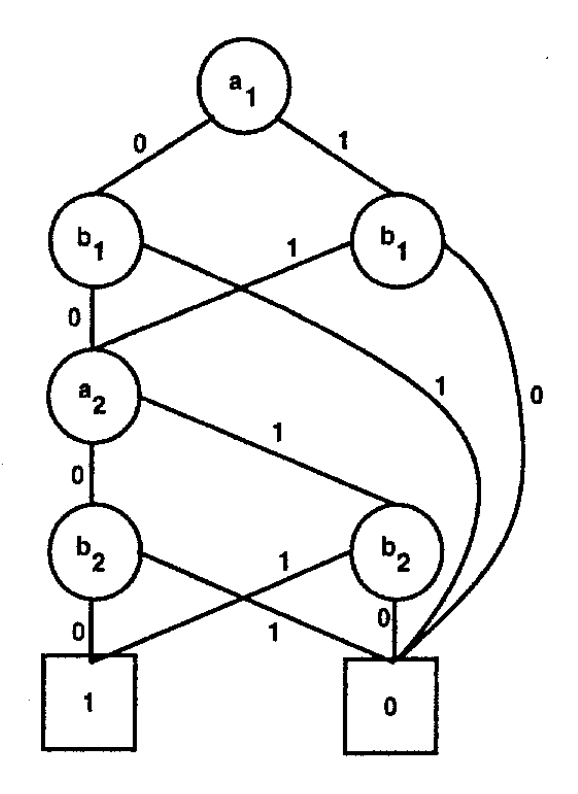
We can also use this to represent relations. The function is set membership.
Kripke structure
Explanation of Kripke structures as detailed here:
Background on model checking
See also
Model checking is the process of checking if a state machine abstract model of a system abides by certain correctness properties. These properties could include “don’t crash” or “don’t double-lock” (i.e., concurrency-related correctness).
To express this in mathematical logic, we use a temporal logic. The temporal is what clues us into the fact that this logic can handle transitions of a state machine over time. Under this temporal logic, the term for state machines is Kripke structures: a structure with different states, transitions between states, and predicates that hold at specific states. We say that a property
holds for a Kripke structure and a path through that structure (a set of states we go through) with the following relation: Notation similarity with axiomatic semantics
Compare this notation with the notation for axiomatic semantics, where for a given program state
and a formula , if holds under , then we can say: In general,
means that under model or assumption , holds.
For a Kripke structure
Any
Computation tree logics
In computation tree logics, we have a number of quantifiers:
- Branching operators:
(all computation paths), (for some computation paths) - Linear time operators:
(“always”), (“sometimes”), (“nexttime”), (“until”)
There are state formulas and path formulas.
Fixpoints
The
TODO
Lots of stuff I’ve skipped over here
Symbolic model checking
We can describe a symbolic model checking algorithm for CTL that takes in CTL formula and returns OBDD corresponding to states of system that satisfy formula.
TODO
And lots of stuff I haven’t finished taking notes on