§ 8. Typed arithmetic expressions

Also recall:
Transclude of pierceTAPL2002#^9c29eb
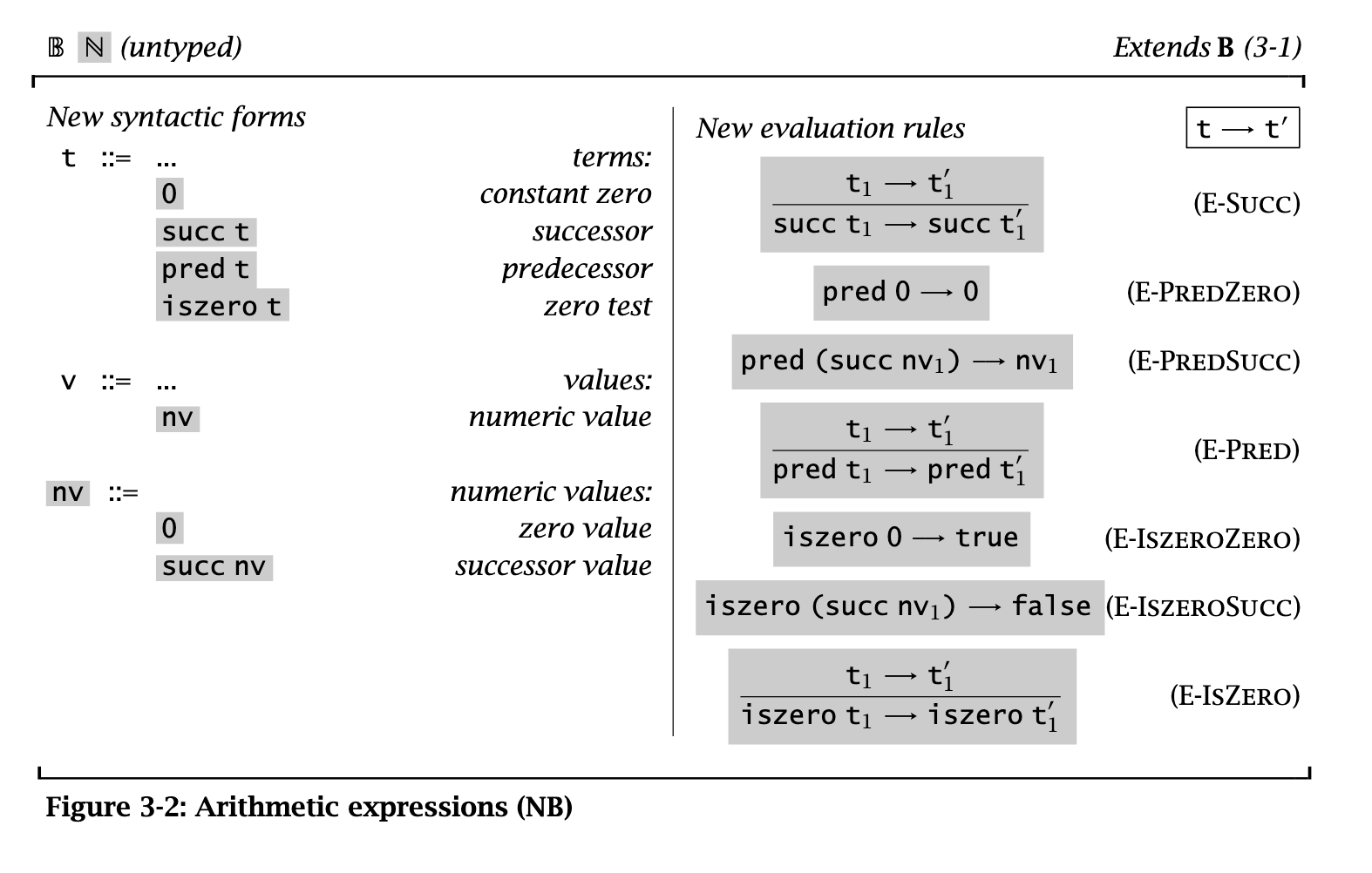
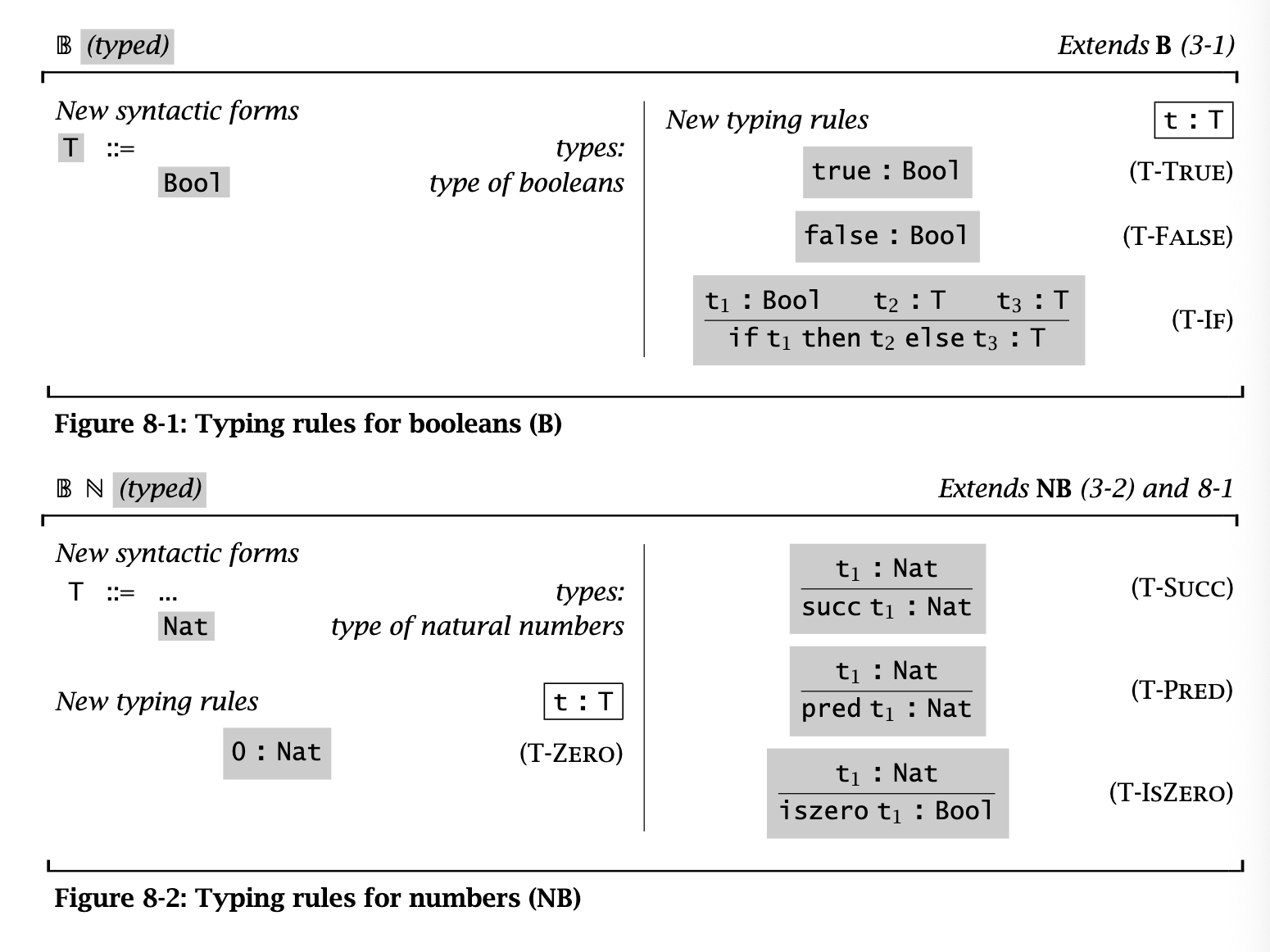
How can we figure out stuck terms (e.g., pred false) without evaluation? For one, we should distinguish between booleans (Bool) and natural numbers (Nat)!
The typing relation
Definition
The typing relation
means that has type . This relation is defined using inference rules, like with evaluation.
- A term is well-typed if
. - The typing relations go from smaller to bigger, for instance:
- Inversely, we can derive lemmas that "invert" this relation, for instance, if `if t1 then t2 else t3 : R`, then the statements `t1 : Bool`, `t2, t3 : R` hold.
- These are *generation lemmas* - they show how to calculate the types of terms!
- These generation lemmas are what we use when building type-checkers are stuff. The derivation rules operate "backwards" to how a type-checker would operate.
-
“statements (aka judgments) are formal assertions about the typing of programs, typing rules are implications between statements, and derivations are deductions based on typing rules”
- Uniqueness of types: each term has at most one type, and one derivation.
- This is not true in the general case (e.g., subtyping)
Here are the typing rules for the arithmetic expr lang:
Type safety = progress + preservation
Definition
What is type safety? Type safety is the property that well-typed terms do not get stuck. We do this basically via induction, using two steps:
- Progress: A well-typed term is not stuck—it’s either a value or can take an evaluation step
- Preservation (aka subject reduction): If a well-typed term takes an evaluation step, the resulting term is also well-typed.
- The resulting term doesn’t necessarily need to have the same type (e.g., in subtyping), but for this example, it should.
To help with proofs, we define the canonical forms of our types—the well-typed values of these types. Think of these like the ADT definition:
data Bool = True | False
data Nat = Z | Succ NatProgress proof for arithmetic exprs
Eval rules
By the structure of the progress proof, let’s assume that
We proceed with induction on the derivation of
- In T-True, T-False, and T-Zero,
is a value, so we’re done. - For T-If, by the induction hypothesis, either
is a value or . - If
is a value, it must be one of the canonical forms for Bool, meaning either E-IfTrue or E-IfFalse applies. - If
, E-If applies. - In either case, an eval step exists.
- If
- For T-Succ, by the induction hypothesis,
is a value or can evaluate to . - If it’s a value, by the canonical forms lemma,
succ t1is also a value (i.e., value by construction) - Otherwise, E-Succ applies.
- If it’s a value, by the canonical forms lemma,
- For T-Pred, by the induction hypothesis,
is a value or can evaluate to . - If it’s a value, by canonical forms lemma, it’s either
0(E-PredZero) orsucc nv1(E-PredSucc) - Otherwise, E-Pred applies.
- If it’s a value, by canonical forms lemma, it’s either
- Same for T-IsZero.
Preservation for arithmetic
Let
Again, we do induction on a derivation of
- In T-True,
t = trueandT = Bool. It’s already a value and there’s no, so it’s true. - Same reasoning applies for T-Zero.
- In T-If, since we know
if t1 then t2 else t3has type, we also must know that and . Since we know that , there are three possible evaluation rules that could apply at this point. - If E-IfTrue applies,
and . from the subderivation, so we’re good. - If E-If applies,
and . By the IH, . Then, by T-If, this whole expr .
- If E-IfTrue applies,
- In T-Succ, there are two possibilities.
- If
is already a value, is a value too and there’s no . - Otherwise, E-Succ applies and
. From T-Succ we know that , and by preservation IH this means . And by T-Succ this means that .
- If
Note
You don’t need to do induction on typing derivations; you can do induction on evaluation derivations too!
- Note that while subject reduction holds, subject expansion doesn’t always hold.
- Evaluation can “erase” ill-typed terms (see here)
- For instance,
t = if true then 0 else false. - By E-IfTrue,
t' = 0, and by canonical lemma,t' : Nat. - But
tis stuck!
- If you’re doing big-step evaluation, swap out
with . - If you have an explicit
wrongterm that is generated whenever you get stuck, progress must evaluate to a non-wrong term.- e.g.,

- e.g.,
§ 9. Simply Typed Lambda-Calculus
We’re gonna look at a version of lambda calculus augmented with primitive booleans and conditionals. We have two type constructors: booleans and arrow (functions).
The Typing Relation
First, let’s define the typing context stuff real quick.
Definition
A typing context
(aka type environment) is a sequence of variables and their types. The comma operator extends by adding a binding on the right. The empty context can be omitted. This context can be conceptualized as a set of pairs, and thus a function/relation (with a domain and range) from variables to types.
Let’s look at the typing judgment for abstractions, T-Abs:
This captures the intuitive statement: “if
We format it the first way because
The other typing rules are straightforward.
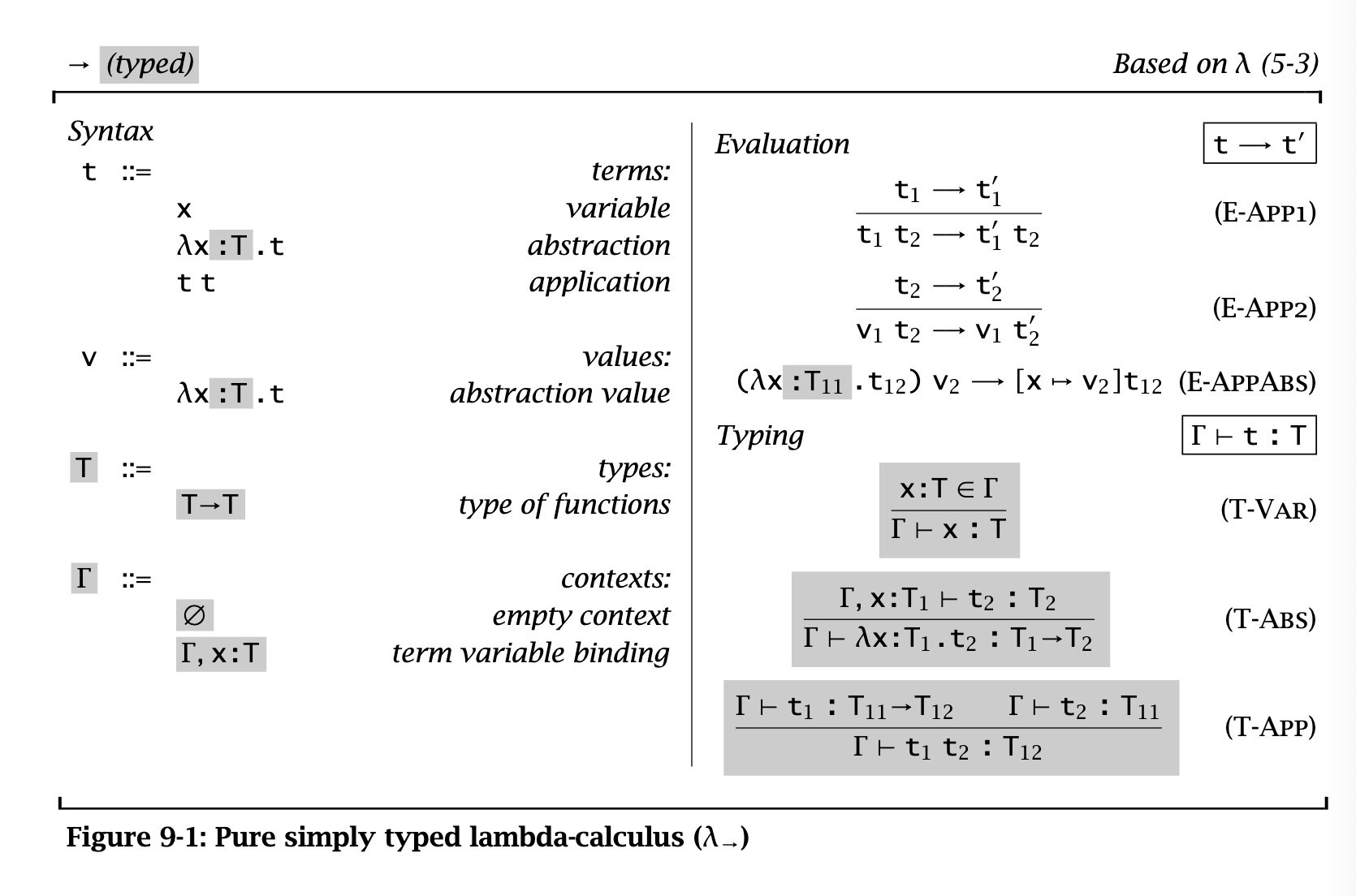
Properties of typing
These are the same lemmas we’ve seen before:
- Inversion: “if a term of this form is well-typed, its subterms must have types of these forms”
- e.g., if
, then and . - Reversing the direction of derivations.
- e.g., if
- Uniqueness: In a given context
, a term with all free variables in must have at most one type. - Canonical forms:
- Bools are true or false
- If
, .
Progress for STLC
We only care about proving progress for closed programs with no free variables (i.e., empty context), since complete programs are always closed. Apparently the proof is similar to Progress proof for arithmetic exprs.
Preservation for STLC
Proving preservation requires a few lemmas first:
- Permutation: you can reorder contexts.
- Weakening: if you have a judgment
, you can add whatever variables you want to and this still holds.
We also show a more ambitious lemma:
- Preservation under substitution: we want to show that if
and , then . ^1b85cb - Let’s do case analysis on the first judgment.
- In T-Var,
must be a variable, since maps from variables to types. - Either
, in which case we already know from the assumptions - Or not, in which case no substitution happens and we’re fine.
- Either
- In T-Abs, we can assume
and . . - We can show
by the induction hypothesis - We do this by weakening
to .
- We do this by weakening
- Thus, by T-Abs,
. - By definition of substitution, running the subst on the whole abstraction is the same as running the subst on its body if
. So we’re good!
- etc.
- In T-Var,
- Let’s do case analysis on the first judgment.
Apparently showing preservation is similar to Preservation for arithmetic at this point.
The Curry-Howard correspondence
- The
type constructor has two kinds of typing rules: - An introduction rule T-Abs showing how elements of this type can be created
- An elimination rule T-App showing how elements of this type can be consumed.
Proofs have very computational vibes!
- Proving
means finding concrete evidence for . - Proving
means, if you’re given this concrete evidence (i.e., a proof) of , transforming it somehow into concrete evidence of . - Proving
means finding both and .
The Curry-Howard correspondence states as follows:
| Logic | PLs |
|---|---|
| propositions | types |
| proposition | type |
| proposition | type |
| proof of proposition | term |
| proposition | type |
Girard’s linear logic led to linear type systems!
Erasure and typability
Compilers normally check types at compile time, then erase them at runtime.
Curry-style vs. Church-style
- In Curry-style, we can talk about evaluation of non-well-typed terms. Semantics is before typing.
- In Church-style, evaluation is only defined on well-typed terms. Typing before semantics.
§ 11. Simple Extensions
These extensions (almost) all introduce derived forms—syntax sugar!
Base types
- Strings? Floats? Things with opaque inner workings.
- We consider these as uninterpreted, unknown, or atomic base types, in the set
with no primitive operations on them at all. - i.e., can’t (de)construct them like nats or anything like that.
Unit type
We add a new constant value
An aside on derived forms
With derived forms, we can either formalize them as new constructs, or as syntax sugar. To prove that something is a derived form (i.e., is basically syntax sugar), we define an elaboration function
iff . iff .
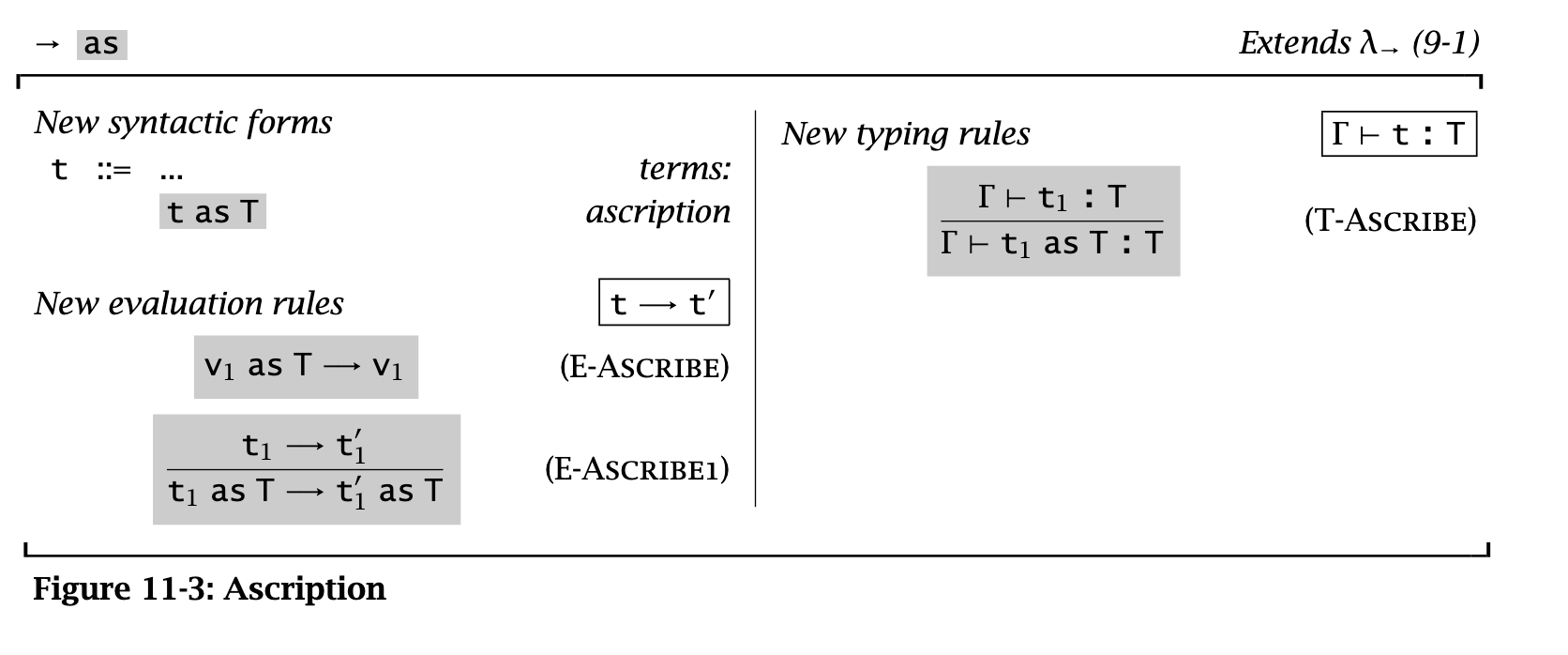
Ascription
Explicitly saying an expression has a type: t as T. Pretty simple.
Let bindings
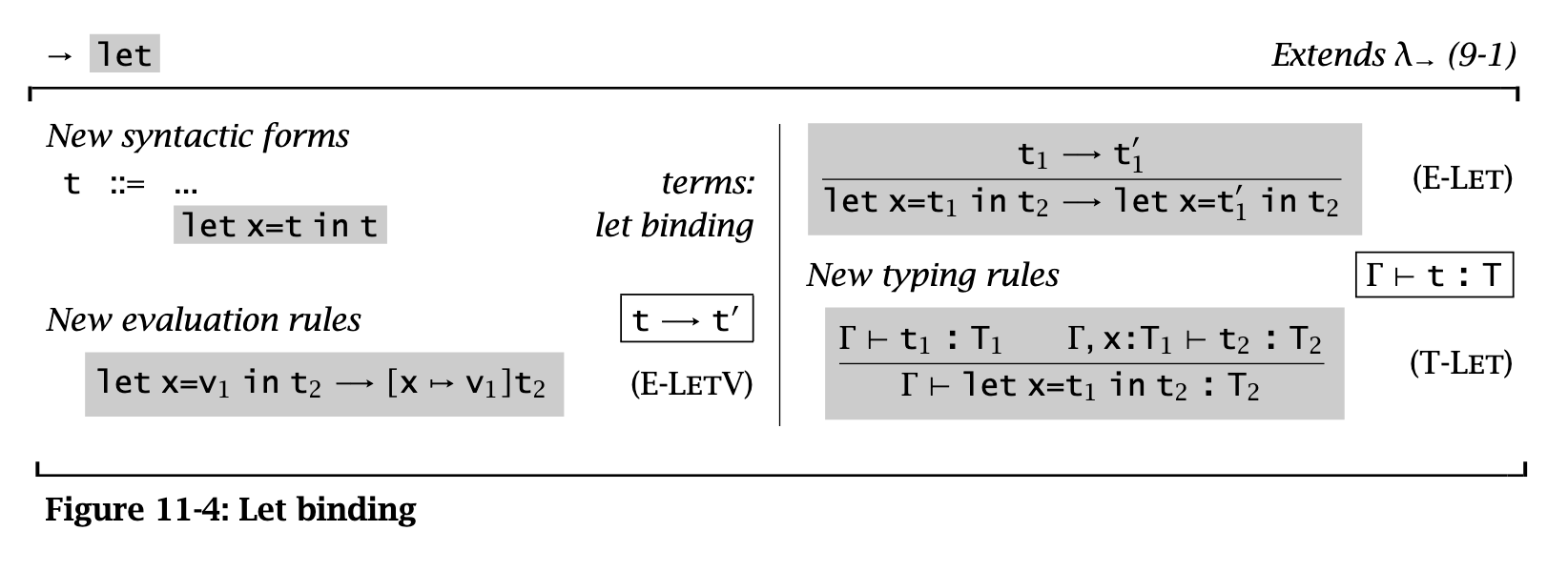
Straightforward. But expressing this as a derived form isn’t so straightforward. Naively, we’d want to do this:
But let into one that uses abstraction and application:

We could define let as immediate substitution, but this changes eval order and erases ill-typed terms.
Tuples & records
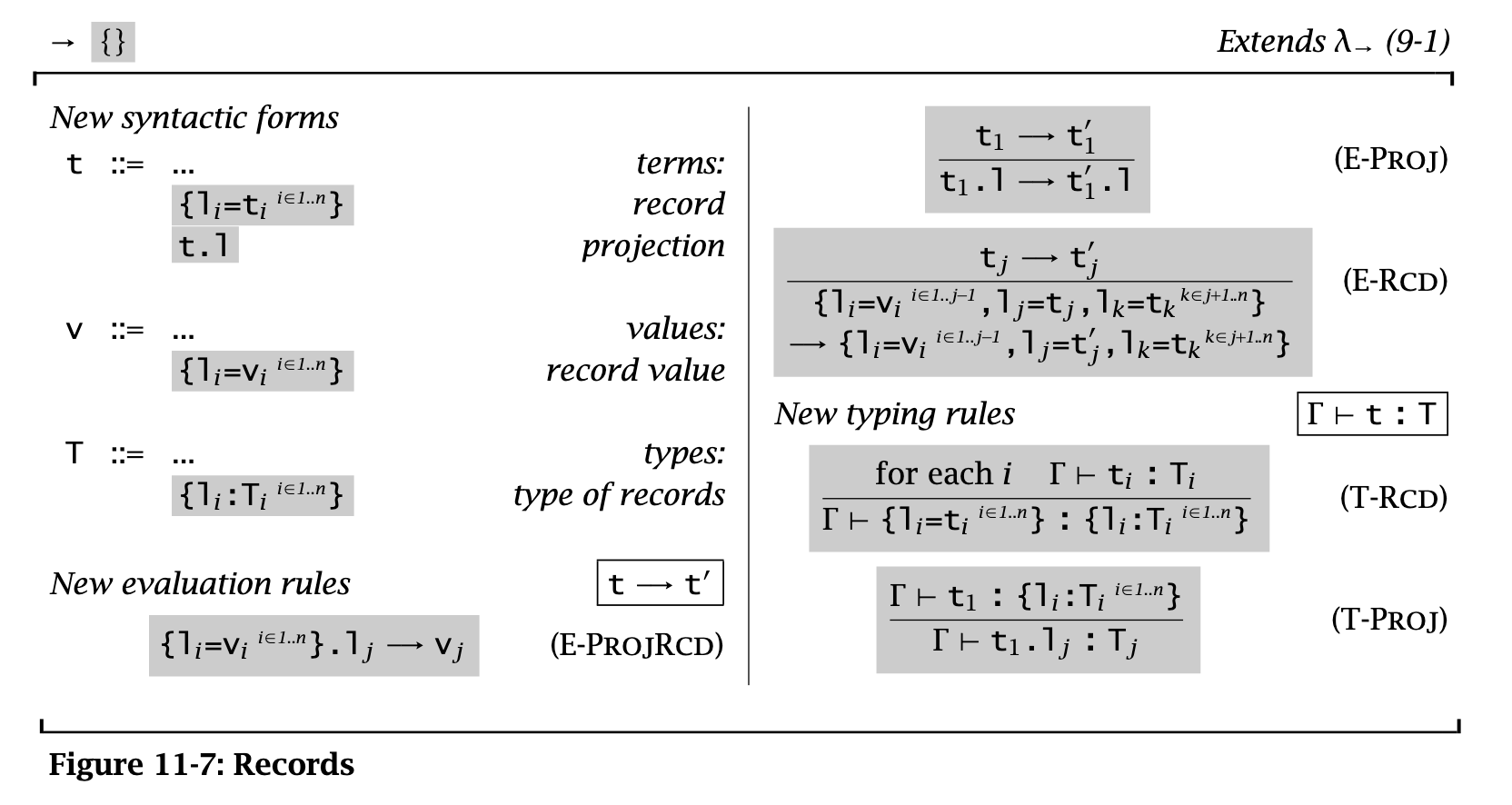
Make note of syntax mostly. Records are the same, except with explicit labels instead of numbered fields.
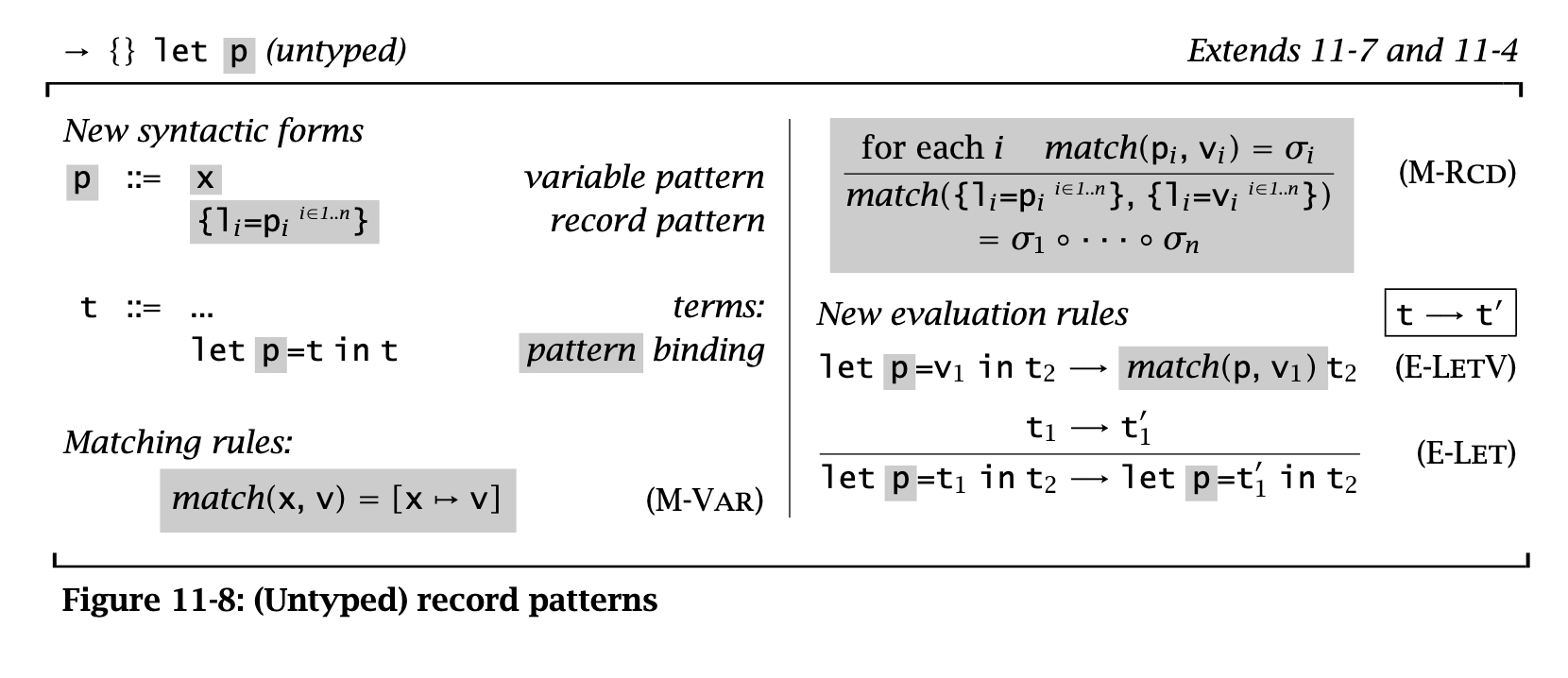
This defines a new match function to generate substitutions through pattern-matched records.
Sums & variants
This is a binary sum type (e.g., data Sum a b = Inl a | Inr b):
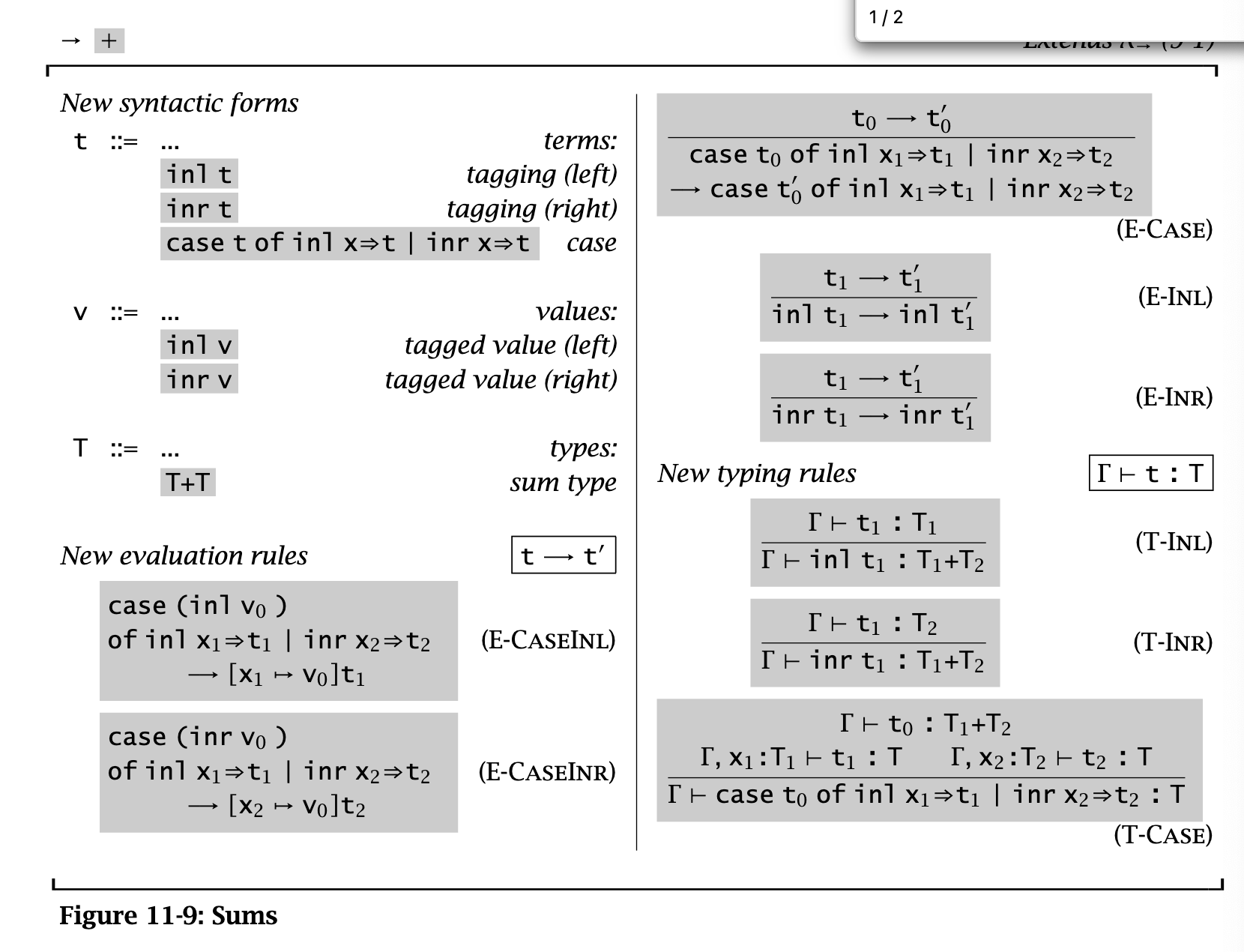
However, sums don’t satisfy uniqueness of types. In T-Inl,
This is the fully general variants:
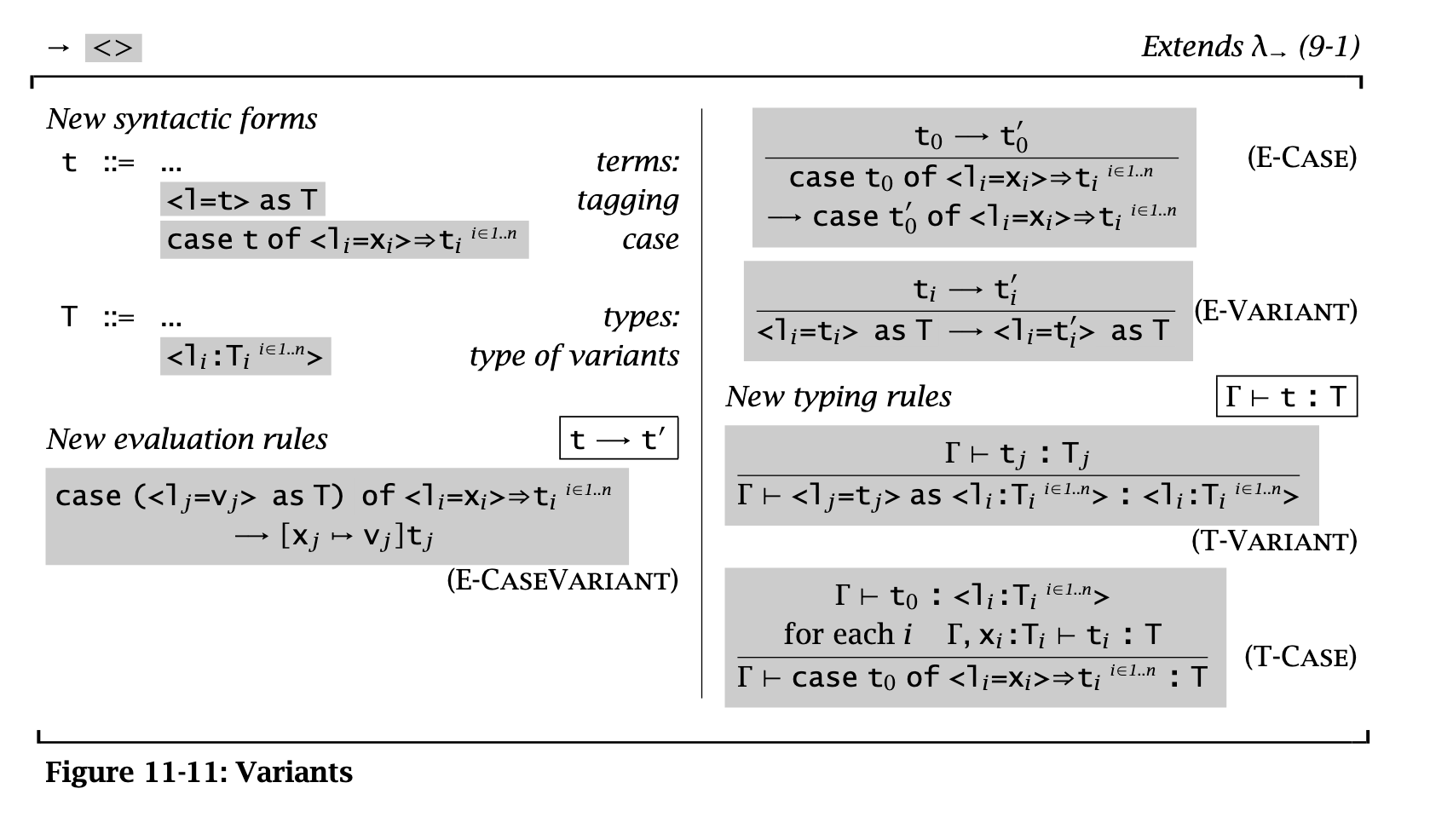
These are analogous to Haskell ADTs with some caveats (variants with one Unit arg don’t need to mention that arg, no parameterized datatypes, no recursive datatypes)
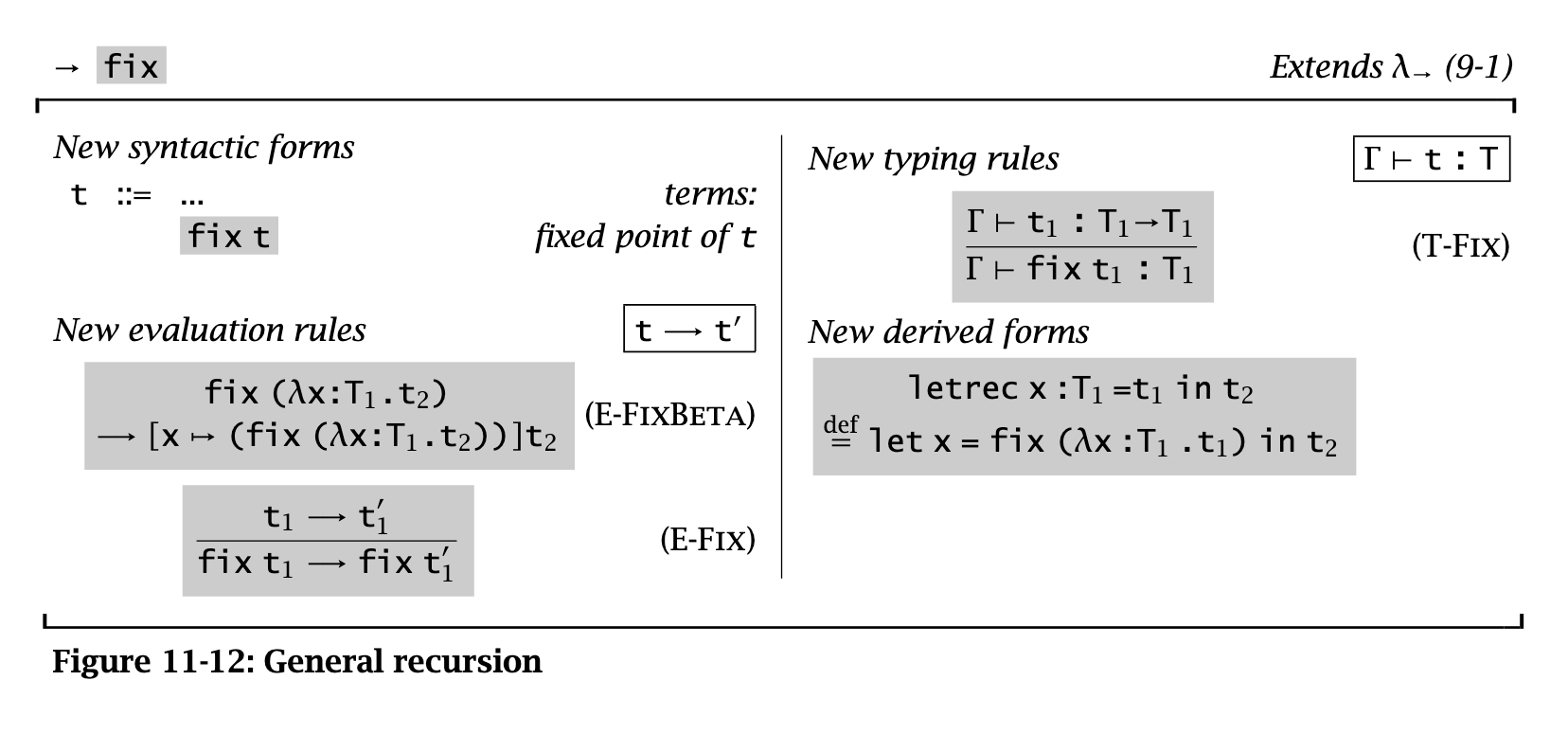
Recursion
The intuition is that the higher-order function ff passed to fix is a generator for the iseven function: if ff is applied to a function ie that approximates the desired behavior of iseven up to some number n (that is, a function that returns correct results on inputs less than or equal to n), then it returns a better approximation to iseven—a function that returns correct results for inputs up to n + 2. Applying fix to this generator returns its fixed point—a function that gives the desired behavior for all inputs n.
fix can’t be defined in STLC (and no non-terminating computation can be typed with only “simple” types). So we add it as an explicit construct: