§ 12. Normalization
Definition
A well-typed term is normalizable or normalizing iff it’s guaranteed to halt in a finite number of steps.
This applies to the simple lambda calculus, but not for many extensions. Additionally, not all type systems are normalizable.
Normalization for simple types
Let’s look at STLC with one base type A. How can we go about proving normalization?
Just doing induction won’t work; if you try doing it the application rule t1 t2, with the IH stating that t1 and t2 are normalized to values v1 and v2, this expression can expand into a bigger expression; we can’t say in general that the term this application expands to is normalizable, since it might be bigger than the original term t1 t2.
To strengthen our IH, let’s first define a set
We want to show that all programs—closed terms of base type—halt. That is to say,
This is an example of a logical relations proof. To prove a property
- Base case: show all terms of type
possess property . - Inductive case: show all terms of type
preserve property . - Then, all terms of type
preserve property of preserving property - etc.
To do this, we define a family of predicates indexed on types—in this case,
The actual proof
Our proof then consists of three parts.
- First, we state that every element of
is normalizable, which is trivial by definition. - Next, we want to show that membership in
is invariant under evaluation, i.e., if and , then iff . - Induction on structure of
. - Nothing to do if
. - If
is an arrow type , there’s more to do - We know
and for some arbitrary . We want to show . - By definition of
, we have . , and from IH, we have . - And by definition of
, .
- We know
- Induction on structure of
- Finally, we want to show every term of type
belongs to . - Induction on typing derivations.
- In lambda abstraction abstraction case, we have
. - We would want to state
by the induction hypothesis (subderivations), but isn’t a closed term! - The solution is just to be like “for all possible substitutions for all vars in the environment of
”: 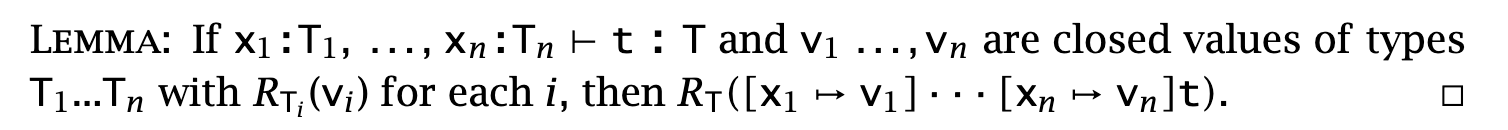
- We would want to state
§ 13. References
In which we start looking at language features involving computational effects (i.e., side effects).
So what are references? Well, they’re basically C pointers, Java object pointers, or Rust Boxes. A reference is a pointer to some location or cell in memory. We define an assignment operator (returning ()) that mutates the value of that memory cell.
r = ref 5; =>
!r => 5
r := 7 => ()
!r => 7
r := succ (!r) => ()
!r => 8
Multiple references can be aliases for the same cell:
r = ref 5;
s = r;
s := succ (!s)
!r => 6
We can have references to functions (boxed functions). For instance, you can define an array of numbers as a Ref (Nat -> Nat). In-place updating the array is assigning a new function to the ref that returns the newly inserted value for the newly mentioned key, and calls the old function at the reference otherwise.
Surface syntax typing
Is straightforward. ref t1 : Ref T1, !t1 : T1, assignment has type ().
Evaluation
This is where things get spicy! We need to model “allocate storage and return a reference to this storage that can be mutated” in our operational semantics.
The answer is to model the heap as a map from an uninterpreted set of store locations
Evaluation depends on a store and can return an updated store. Thus, single-step evaluation is now
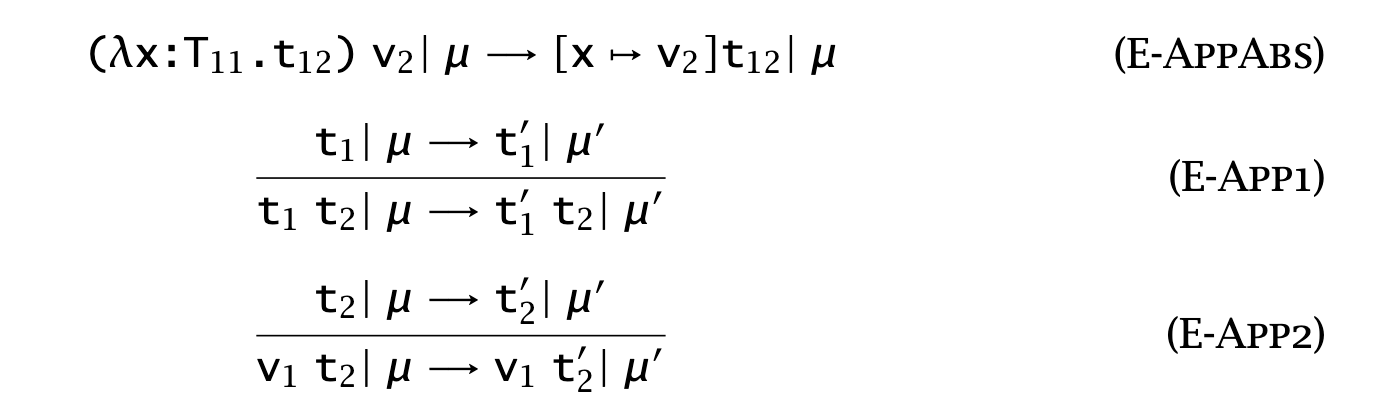
Function application itself has no side effects, and in the other cases we propagate side effects.
Values (and thus terms, since all values are terms) include a store location l. This doesn’t mean the surface syntax should involve explicitly using store locations; this term language is an IR basically.
So let’s formalize evaluation.
First, dereferencing a term !t1 means evaluating t1 until it becomes a value.
Then, dereferencing is just getting the value from the store.
Next, evaluating an assignment expression t1 := t2 means evaluating both sides until they become values.
Assignment just means mutating the store (when we prove type safety, we will show that
To evaluate creation of references, we first require that ref t1’s t1 is fully evaluated. Then:
Location and store typing
So now that we have locations in the mix, what’s the type of that? The most obvious answer would be to do something like this:
Naive rule
This intuitively makes sense; given the store as additional context, the type of a location is Ref T1, where T1 is the type of whatever l points to in the store.
However, this definition actually sucks for two reasons:
- It makes type checking hard. Finding the type of
requires finding the type of the value it points to every time it’s mentioned. If this value itself contains locations, those locations will also have to have their value types recalculated on every mention - It makes cyclic references impossible to type-check.
has no finite type derivation given store , since finding the type of means finding the type of , which depends on .
Intuitively, we know that when we create a location, that location will only ever have one type. If you create a ref 5, you can’t assign true to it later on! So instead, we create a store typing function
Notice that the store typing isn’t in the context at the top. Unlike the first rule, which says “given
The typing rules from Surface syntax typing remain unchanged; we just also thread in

Note
Alternatively, you could imagine
refas a syntax sugar maybe?
Safety (and mostly preservation)
Progress (closed, well-typed terms are either values or have an eval step available) is somewhat straightforward; just extend induction on typing derivations. Preservation is where the real sauce is!
First, we need to explicitly tie a store
Remember that preservation means if a well-typed term takes an evaluation step, the new term is also well-typed. Since we have a store to deal with, we must also assert the well-typedness of the store before and after too. Thus, we want to show:
For the proof, we first show preservation under substitution (done in the same way as with STLC):
We also show that replacing the contents of a cell in a store with a new value of correct type doesn’t change the type of the store:

Finally, we include a “store weakening” lemma that states that if a store is extended with a new location, the extended store covers everything the original does. Shown by induction.
With all these, we can show preservation.
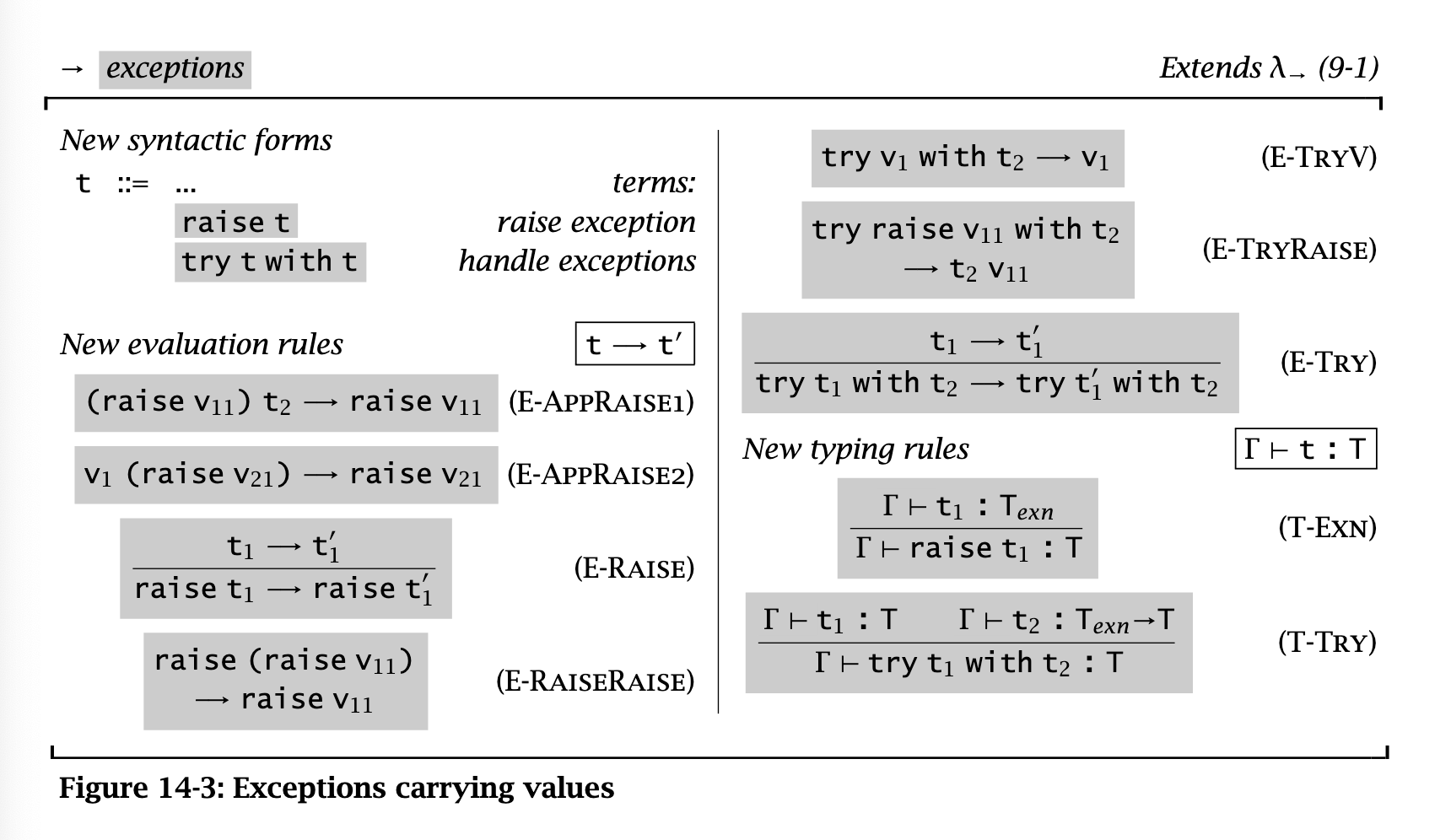
§ 14. Exceptions
How can we model exceptions in our language?
Abort immediately
First, the simplest kind of exception: give up immediately.
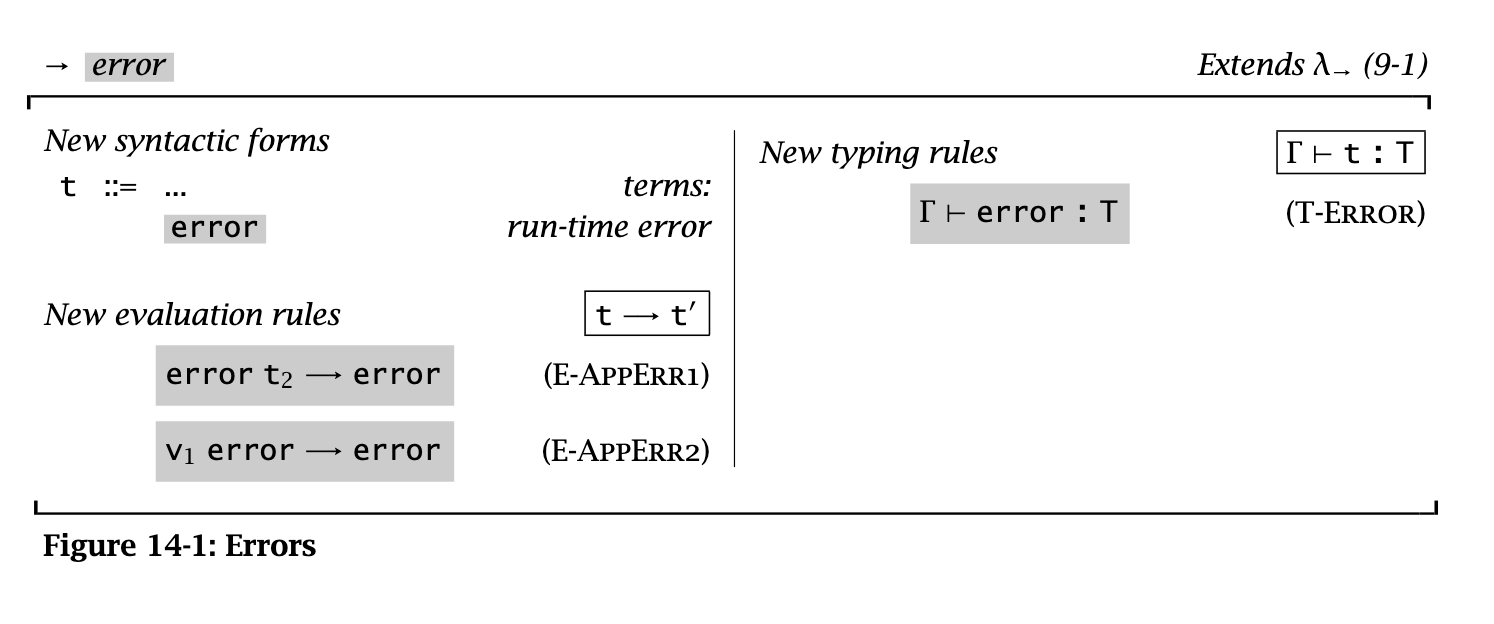
In this formalization, errors are terms but not values. This means there’s no ambiguity in evaluating an expr like error means we no longer have uniqueness; we can alleviate this through either subtyping or parametric polymorphism.
When showing progress, we now want to show that an expr becomes either a value or error.
try-catch
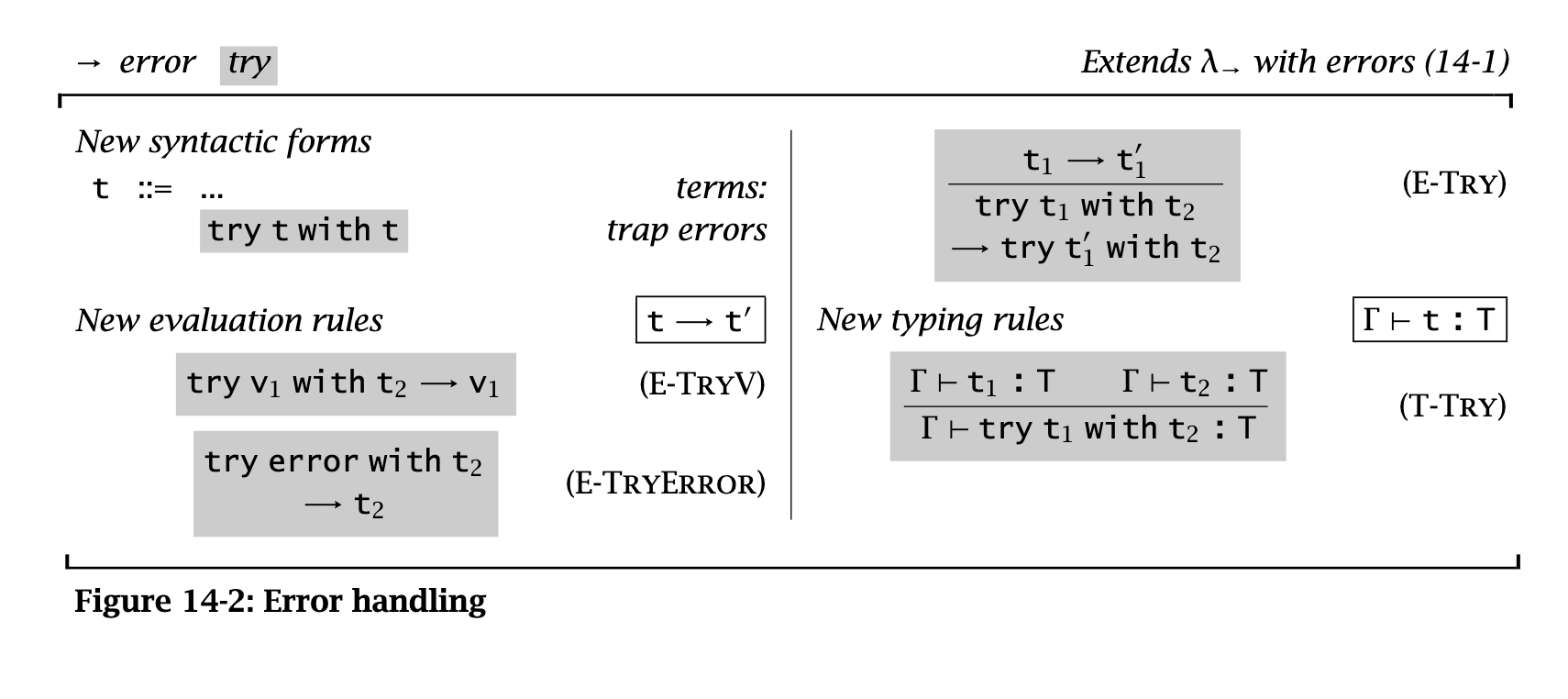
exceptions with values