pierceTAPL15182002

§ 15. Subtyping

Subtyping is a more fundamental change to how our language is typed. It’s normally associated with OOP stuff, but in this section we look at how subtyping applies to function and record types, since a lot of interesting subtyping-related stuff happens here already!

In particular, we might want a record {x = 0, y = 1} to work as an argument to a function that takes {x : Nat}.

Subsumption

The principle of safe substitution

One definition of the subtyping relation is that any term of type can be used where a type is expected. This is the principle of safe substitution.

Another intuition is that every value described by is also described by . This subset semantics is mostly sufficient.

We formalize the subtyping relation with respect to the typing relation with the rule of subsumption:

The subtype relation

This relation is formalized as a bunch of inference rules for deriving statements of the form (i.e., is a subtype of ). Straightforwardly, subtyping is reflexive and transitive.

For records, we have three subtyping rules. First, we have the width subtyping rule, which intuitively states that more specific record types (i.e., records with more fields) are subtypes of less specific record types:

Second, we have the depth subtyping rule, which states that the types of individual fields between records can vary, so long as they are correspondingly subtypes:

Finally, we have a record permutation subtyping rule, which just states that order of record fields doesn’t matter.

Function/arrow types have a slightly counterintuitive subtyping rule:

Remember that the core intuition of subtyping is: “if can be used wherever can be used, .” Arrow types are contravariant on the argument type (the subtype relation is reversed) because to ensure that can be used wherever is, must take at least as many possible arguments that can. Then, following intuition, arrow types are covariant on the return type.

Properties of subtyping & typing

In which we prove preservation and progress.

TODO

Left as an exercise for the reader lmao

Top and Bottom

• Why Top?
  • It’s basically Object in Java, etc.
  • It’s useful when combining subtyping with parametric polymorphism
• Why Bottom?
  • Corresponds to the never type !/Infallible in Rust
  • Can’t be constructed, can be the result for error values.

Subtyping & other features

Ascription

Without subtyping, it’s basically just documentation and a guide to a compiler for how to print types. But with subtyping, we can do some real interesting shit! Java-type shit.

For instance, we can upcast a type to its supertype. In our typing judgments, this means combining a straightforward typing judgment and a subtype judgment:

Less straightforwardly, we can downcast a type to its subtype. At compile time, we just believe the user:

Then in our semantics, we only evaluate an ascription if, at runtime, the expression has the correct type:

This loses us progress, since a well-typed term might get stuck evaluating an erroneous type ascription. However, we can recover that back by either throwing an error or replacing downcasting with a type-testing operator (e.g.., Python’s is operator):

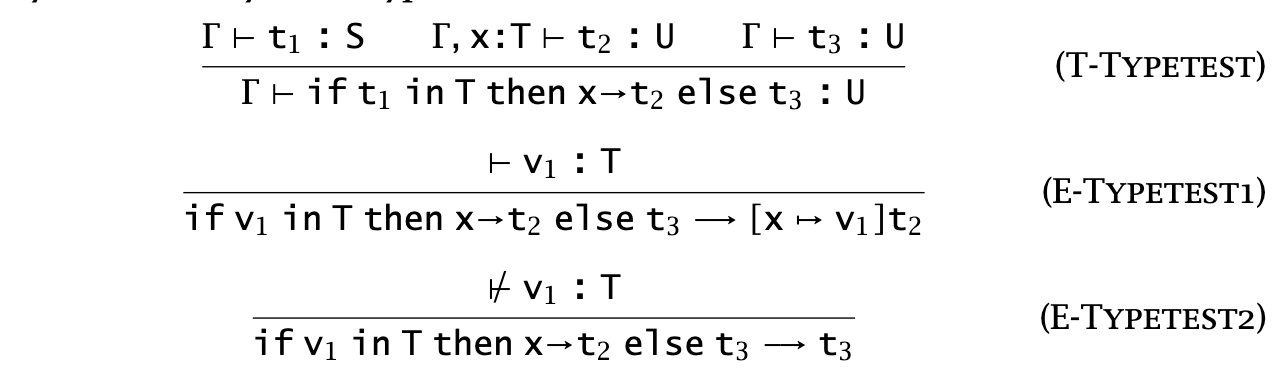
You can use this to imitate generics, Go-style. Additionally, Java uses downcasting for reflection—loading a bytecode file and creating an instance of some class it contains, then downcasting the Object into a know class.

To avoid having to do full type-checking in the evaluator, we can use type tags which “capture a runtime ‘residue’ of compile-time types and that are sufficient to perform dynamic subtype tests.”

Variants

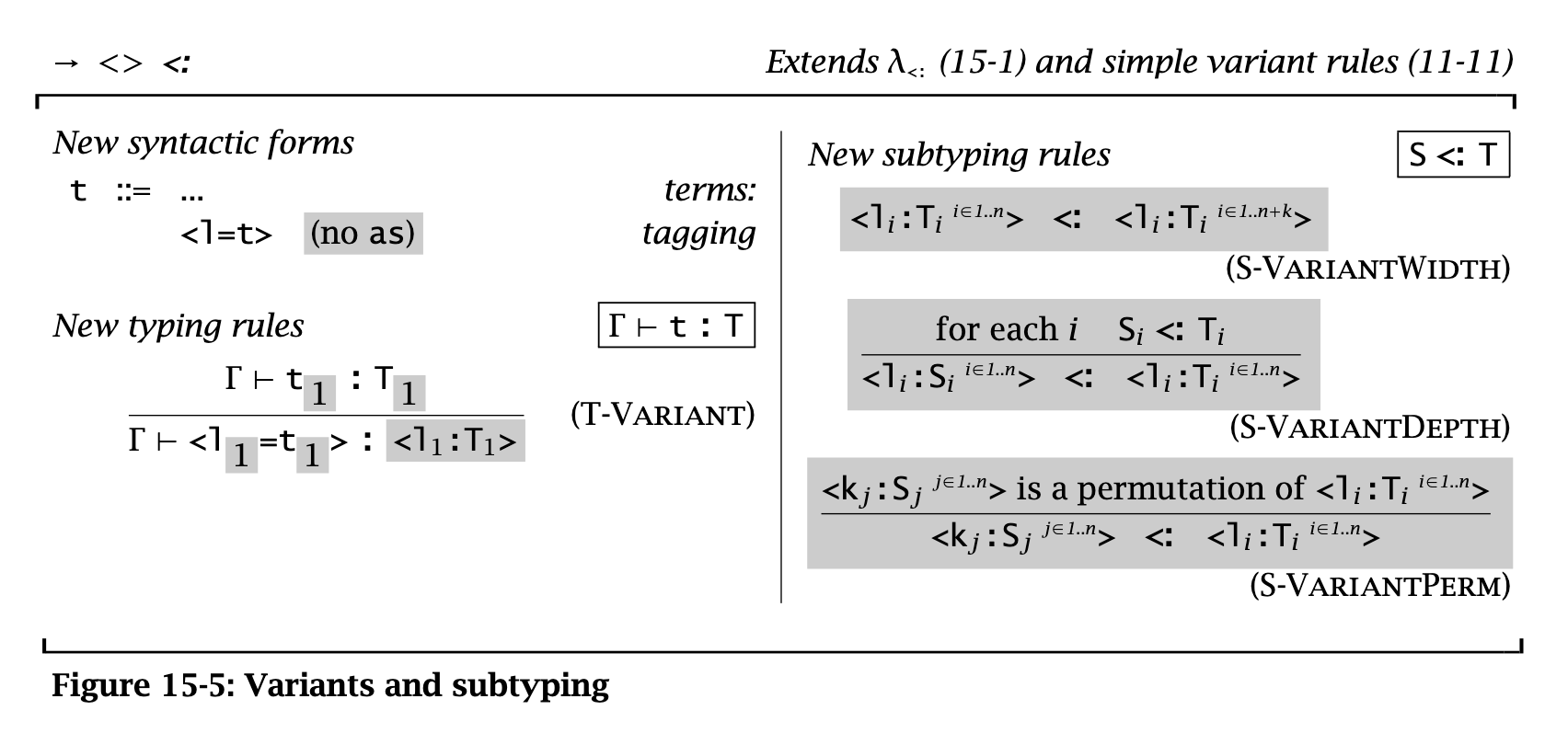
Similar to records, but variant types with fewer variants are subtypes of those with more.

References

An example where a type constructor isn’t covariant or contravariant, but invariant:

We still involve subtyping stuff so we can do field/variant reordering and all that, but we demand that and are otherwise equivalent. This is because when reading, we need , but when writing, we need .

Alternatively, you can break up Ref into two constructors with unique capabilities: reading from a Source and writing to a Sink. Each of these constructors is co- and contravariant, respectively, and are supertypes of Ref, which contains both of these capabilities.

Coercion semantics

Currently, we have a subset semantics for subtyping: a subtype contains a subset of the literal values of its supertype. However, in reality, this doesn’t always apply. With number values, for instance, we might want to say even though Ints and Floats have very different representations. And for record types, we might want to implement more efficient projection that uses the type of a record to determine where a field is located in memory; this would work if not for the permutation rule!

Instead, we can “compile away” subtyping to runtime coercions; e.g., if an Int is promoted to a Float during typechecking, then at runtime we change this number’s repr. This coercion semantics is expressed as a function transforming terms and types of a language into a language without subtyping.

Notation

TAPL uses the syntax for two related, but distinct, functions: the function that transforms types, and the function that transforms terms.

Translating types is pretty straightforward: Top becomes (), [[T1 -> T2]] = [[T1]] -> [[T2]], etc.

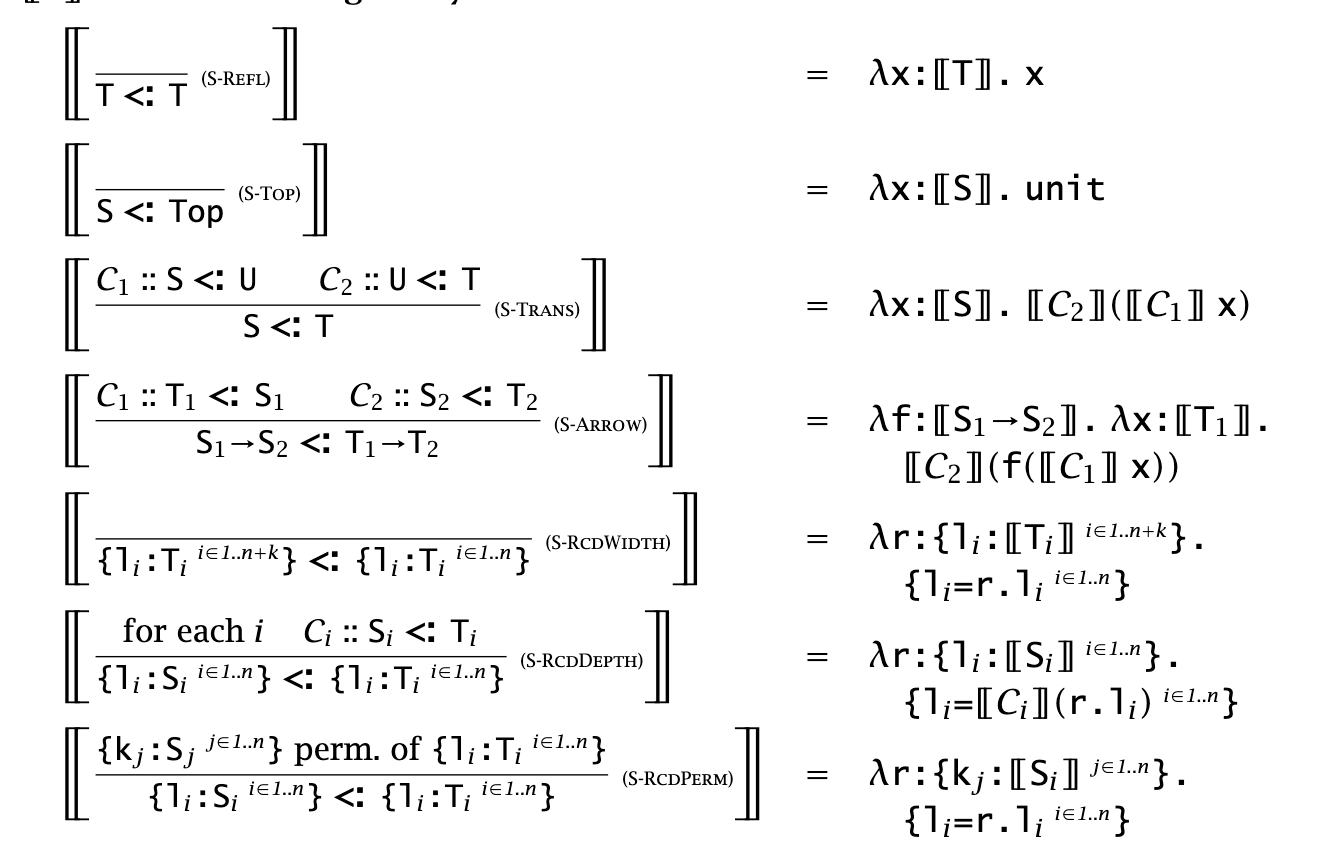
Translating terms is more complicated. Since translating a term requires knowing what typing judgments were used to figure out where to put coercions, the coercion semantics operates on derivations, instead of terms themselves. When operating on a subtyping derivation for the subtyping statement , the translation returns a function that takes in a value of type and returns a value of type .

Notation

TAPL represents the functions that actually coerce a value to type as .

When operating on a typing derivation of the statement , the translation is a target-language term of type .

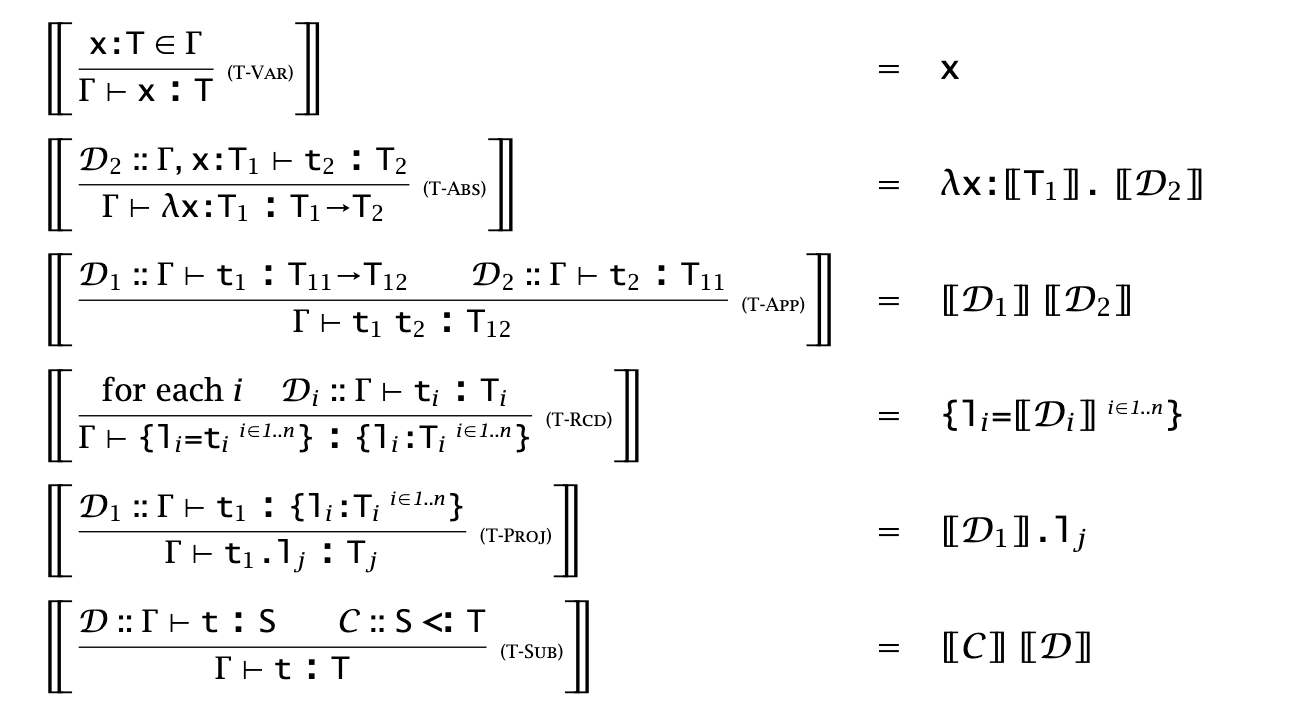
The important thing to note here is when we encounter a type judgment that results from application of subsumption , we call the coercion function generated by on the result of translating the rest of the term.

With this defined, we define type rules on the high-level language, but semantics on the low-level language only.

Coherence

One more wrinkle: depending on how primitive types are subtyped, we might get multiple valid derivations for a term. For instance, if you have Bool <: Int, Bool <: Float, and both Int and Float <: String, for (λx : String. x) true, you can get different results depending on how true is converted. This is called coherence.

Definition

A translation is coherent if for every pair of derivations and with the same conclusion , the translations and are behaviorally equivalent.

Intersection and union types

An intersection type is inhabited by terms belonging to both and .

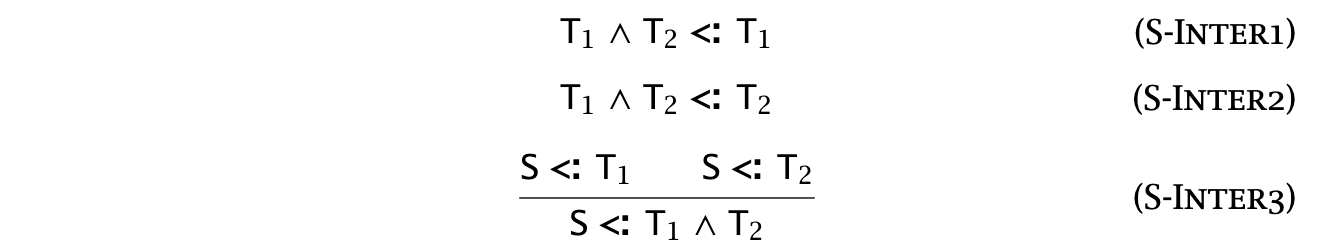
For functions, we also have:

The intuition behind this rule is that, if we know a term has the function types S→T1 and S→T2, then we can certainly pass it an S and expect to get back both a T1 and a T2.

In a lazy untyped lambda calculus, a term is typable iff its evaluation terminates.

TODO

How?

We also have union types, . Union[int, str].

§ 18. Case Study: Imperative Objects

We’re gonna model objects/classes, à la Smalltalk or Java, in LC! Specifically, we’re gonna model a Counter object that can be read or incremented.

What is OOP?

TAPL characterizes the fundamental characteristics of OOP as:

• Multiple representations: where a conventional abstract data type (ADT) is a set of values and a single implementation of operations on these values, two objects responding to the same set of ops can have entirely different internal reprs, as long as they have methods that fulfill that interface.
• Encapsulation: object’s internals are hidden
• Subtyping: an object’s interface—its type—is the set of names and types of its ops. Internals aren’t mentioned
• Inheritance: classes and subclasses that inherit behavior.
• Open recursion: Using self to invoke method defined later in class.

Objects

An object is a record of functions, where internal state is represented by a reference:

c = let x = ref l in
      {get = λ_:(). !x,
       inc = λ_:(). x := succ(!x)}

c isn’t a factory/ctor, it is an instance of the counter. Then, a Counter is the type {get : Unit -> Unit, inc : Unit -> Unit}. A factory just wraps this in another lambda:

newCounter = 
  λ_:(). let x = ref l in
           {get = λ_:(). !x,
            inc = λ_:(). x := succ(!x)}

Subtyping

Because of how we’ve implemented record types, you can add another method and it’ll still fulfill the original record type!

An aside on nominal v. structural type systems

A nominal type system is a system where names matter. For instance, if you defined two classes with the same fields fst : Int, snd : Int, they would not be equivalent, since they’re named different.

A structural type system operates directly on the structure of types. Thus, two classes (or indeed, two records) with the same fields would be considered equivalent.

See §19.3 for further discussion of this topic.

Grouping instance variables

Make state a record instead of just a single value. This record is the representation type.

c = let r = {x=ref 1} in
      {get = λ_:Unit. !(r.x),
       inc = λ_:Unit. r.x:=succ(!(r.x))};

Classes

In its most primitive form, a class is simply a data structure holding a collection of methods that can either be instantiated to yield a fresh object or extended to yield another class.

The key special sauce of classes is abstracting methods with respect to their representation. In our case, that means abstracting the methods of a counter from the specific state record used to represent it.

counterClass =
  λr:CounterRep.
    {get = λ_:Unit. !(r.x),
     inc = λ_:Unit. r.x:=succ(!(r.x))};

CounterRep is the representation type from before. Then, creating a new counter just means instantiating this class with a record. We can use this to kinda do subclasses:

resetCounterClass =
  λr:CounterRep. let super = counterClass r in
    {get = super.get,
     inc = super.inc,
     reset = λ_:Unit. r.x:=1};

Instance variables

What about subclasses that want to add extra instance variables? Change the type of the representation (such that it’s a subtype of CounterRep!)

BackupCounter = {
  get : Unit→Nat,
  inc : Unit→Unit,
  reset : Unit→Unit,
  backup : Unit→Unit};

backupCounterClass =
  λr:BackupCounterRep. let super = resetCounterClass r in
    {get = super.get,
     inc = super.inc,
     reset = λ_:Unit. r.x:=!(r.b),
     backup = λ_:Unit. r.b:=!(r.x)};

Superclass methods

We can call superclass methods in the body to extend superclass behavior.

Self

To get self, we use recursion.

setCounterClass =
  λr:CounterRep. λself: SetCounter.
    {get = λ_:Unit. !(r.x), set = λi:Nat. r.x:=i, inc = λ_:Unit. self.set (succ(self.get unit))};

The class now takes an instance of self as an argument! We then use fix during instantiation to do the recursion stuff.

newSetCounter = λ_:Unit. let r = {x=ref 1} in fix (setCounterClass r);

This is open recursion. We could put fix in the class defn, but doing this instead allows self to be a subclass of the current class!

Self, part 2

That definition actually diverges. To fix this, we need self in the class definition to be a thunk: Unit -> SetCounter.

However, now this means that the methods for a class are recalculated on every recursive call. Instead, what we can do is allocate a reference to the record of functions, assigning a dummy initial value, then assigning the ref to the result of calling setCounterClass:

newSetCounter =
  λ_:Unit.
    let r = {x=ref 1} in
    let cAux = ref dummySetCounter in
    (cAux := (setCounterClass r cAux); !cAux);