sridharanAliasAnalysisObjectOriented2013

See also

This video lecture from Adrian Sampson for Cornell CS 6120 and this page on Pointer Analysis for CS 701 at Wisconsin.

Who cares? Motivating analyses

See also

This combines info from §2 of the paper and the CS 6120 lecture.

Anything that’s “easy” with stack variables is difficult in the presence of (heap) pointers, without knowing something about aliasing: if two pointers actually point to the same value in memory at program point , or if they point to different values.

We need to know about alias analysis when doing:

• Eliminating dead stores to a pointer: what if an alias reads the location later?
• Propagating stores through loads: normally we could do *x = 4; *y = 6; 4 + *x into *y = 6; 4 + 4. But if x = y, we can’t do this!
• Loop-invariant code motion: what if an alias modifies this value and it’s not invariant in the loop condition?
• Auto parallelization: we can’t be sure that two seem parallelizable procedures actually don’t touch each other’s state if their pointers alias
• Calculating resource leaks: often we want to do automated resource leak analysis in languages like Java.
  • If we do this.a = Resource(); t1 = this.a; free(t1), we need our analysis to know that the resource was freed!

Figuring out if two pointers will alias at any given point is undecidable, and the answer might be sometimes! Thus, often we consider approximations that provide may-alias analysis: they tell us if two pointers may alias, but not if they must. However, this does guarantee that pointers do not alias!

In this paper, we examine two forms of alias analysis:

1. Points-to analysis, which is a flow-insensitive may-alias analysis.
2. Access-path tracking, which is a flow-sensitive must-alias analysis.

On flow-sensitivity and -insensitivity

In this note, we will discuss what it means to be flow-sensitive or -insensitive. However, it might also be useful to look at Principles of Program Analysis 3: Constraint-based analysis and how they discuss flow-sensitivity in the context of control flow analysis.

Points-to analysis

A points-to analysis is an over-approximation of the heap locations a program pointer (a variable or a pointer in a heap-allocated object, like an instance field) might point to. At some program point, given two variables and , if they may potentially point to the same pointer according to this analysis—that is, the intersection between their set of possible heap locations is non-empty—then they may alias.

Dataflow framework

Following the CS 6120 lecture, let’s express a points-to analysis as a dataflow framework in the style of Dragon Book 9: Machine-independent optimization. We define our dataflow framework as follows:

• The direction is forward.
• Our analysis value is a mapping from variables to heap locations they may point to. Thus, the domain is the set of mappings from variables to sets of heap locations:
• The meet operation is union on variables and the locations they can refer to.
• Our transfer function pattern matches on the statement .
  • l = const K:
  • l = alias y:
  • l = new y: , where is a fresh location.

We say that two variables and may alias if, given dataflow analysis value , .

This analysis is flow-insensitive: the analysis value of statements doesn’t actually depend on the order they’re in! Indeed, because of how dataflow analysis iteratively propagates, reordering or repeating statements won’t change the result of the analysis (even if it results in nonsense programs).

Constraint-based framework

We can equivalently express this dataflow analysis in terms of constraints generated by inference rules:

statement	constraint
i: x = new T()
x = y
x = y.f

| | x.f = y |

| where is the analysis value for some variable. The last two rules basically just do a “forall” with field access.

Some properties about this analysis:

• Like the above, it’s flow-insensitive. They’re saying equivalent things! is saying the same as : the analysis for must include the analysis for !
• It’s field-sensitive. We can reason separately about each instance field of each abstract location. This is important for languages like Java (ugh lmao)
• It’s context-insensitive. Every method call is must receive the same analysis, regardless of context. See the next section.

Context sensitivity

Consider the following example program:

id(p) { return p; }
o1 = new Object();
o2 = new Object();
a = id(o1);
b = id(o2);

With our current analysis, a function can only have one analysis, regardless of the calling context. Thus, we are forced to assume that id could potentially take both o1 or o2 as an argument. Thus, id can return either o1 or o2, and a and b may alias.

In a context-sensitive analysis, we provide a distinct context for each call site. This process analyzes each call of id separately for each of its call sites, and can conclude that id only can return o1 in its first call, and o2 in its second call, meaning a and b can’t alias!

Parallels with -CFAs and -CFAs

This is essentially an alternate formulation of -CFAs and -CFAs.

As we go on, we’ll be drawing parallels between this treatment of context-sensitivity and that of control flow analysis of functional programs.

Our formulation of this analysis assumes we’re reaching statements inside a method . We define as the set of contexts arisen for all calls of ; we can think of as the current environment in /-CFA land. Our analysis takes an abstract pointer as an argument now, instead of just , and the analysis value is a pair of pointer location and context, just like with -CFAs (remember that with -CFAs, the context environment is a context).

Our formulation of this analysis is generic over two functions, which specify a context-sensitivity policy:

• The selector function determines what context to use for a callee at a call site.
• The heapSelector function determines what context to store when we come across a new allocation.

Let’s break this down.

• The first four rules just thread context information. new uses heapSelector to compute the stored context.
  • When , we have context-sensitive analysis.
  • When , we have context-insensitive analysis.
• The Invoke rule is a doozy lmao
  • The first two lines deal with virtual dispatch, calculating the true method.
  • The include analyses for r and a_1 thru a_n.
  • The selector function builds our new context.
    • It takes the method being called , current context, call site , and , returning the new context for a method.
    • In a context-insensitive analysis, selector just returns .
    • In -CFA, selector returns .
  • This new context must be in the contexts for .
  • The other rules propagate analyses from arguments to formal parameters.
    • Formal parameter must include arguments.
    • x must include return.
    • Remember the constraint flow rule-of-thumb!

Object sensitivity

Instead of distinguishing method calls by call strings, in object-sensitive analysis, we extend our context with self on every method call! The intuition is that this should be able to distinguish between identical operations performed on different self objects. Here, our context is no longer a list of call sites, but a set of locations—the different self objects that have had methods called on them in the process of getting to this expression:

The precision of this analysis is incomparable to that of call-string-sensitive analysis. They’re good at different things. People often combine them; use the other for static methods, this otherwise.

We can also do type-sensitivity, where we record the types of the enclosing class for the allocation site. This is kinda as accurate as object sensitivity, but is more scalable.

Cartesian Product Algorithm

What if we don’t limit our attention to just self, but look at all arguments? Indeed, since the analysis of each argument is a set, what if we look at the cartesian product between all of our arguments?

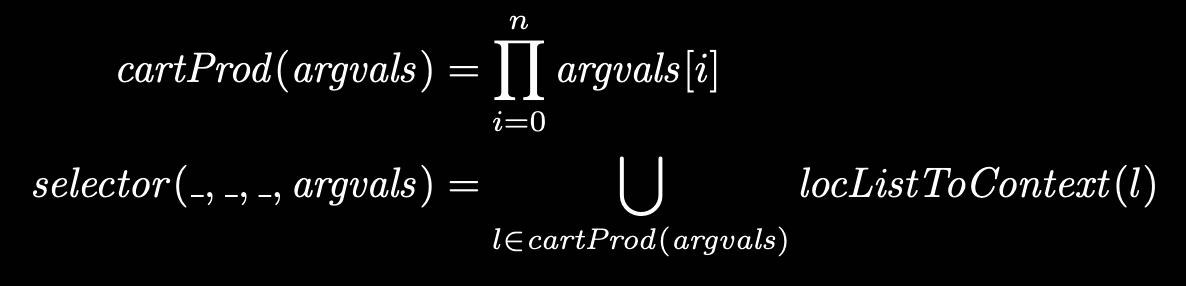
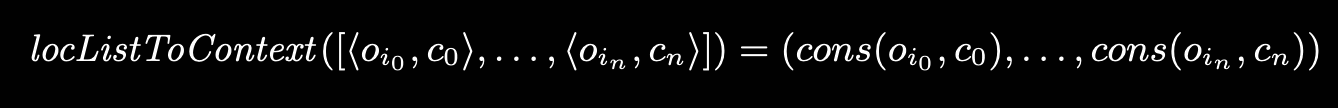
Originally used for type inference, since it’s way less scalable for actual object values.

Unification-based approaches

If we have equality instead of subset constraints, we can use fast union-find data structures to represent equal points-to sets. This works for C++ programs but not Java, since Java requires virtual dispatch.

Note

Another example of unification stuff. See semantic analysis.

Implementation

To implement this analysis, we express the analysis as a graph reachability problem, similar to how we can solve other program analysis problems (e.g., similar to solving CFA constraints). Here, the graph has an edge iff one of the following holds:

• is an abstraction location representing a statement x = new T(), and is x.
• .

Since we want to essentially find what nodes are reachable from source nodes , this is called a transitive closure problem. Transitive closure means—in the abstract—adding edges from nodes to transitively reachable nodes. Additionally, this is a dynamic transitive closure problem, since we can only add edges once existing edges have been traversed.

Note

This is an instance of

The actual algorithm doesn’t involve adding edges for transitive closures, and instead mirrors the CFA graph-based analysis:

• Iterate through statements.
• When an edge hasn’t been added, we add it and do difference propagation from source to target
  • Only add abstract locations where that reachability info hasn’t propagated to successors
• Add successors to worklist where successors change

This is . We can do some small optimizations to make this faster too.

• Type filters
  • Label edges as requiring subtype of or exactly .
  • x = (T) y requires for a subtype of .
  • Only add appropriately-typed objects to points-to sets.
  • Bit-vector intersection
• Cycle elimination
  • If we have a = b; b = c; c = b;, these will all have the same set. Collapse them to one node!
• Method-local state
  • For variables that don’t point to method arguments, don’t use global constraint system to compute them, and compute on-demand. Space savings!
  • Separate local state!

How to implement better context sensitivity

How can we represent points-to sets and relevant structures in a more efficient way?

• Shared bit-vectors (Heintze, N.: Analysis of Large Code Bases: The Compile-Link-Analyze Model (Draft of November 12, 1999)
• Binary decision diagrams: representation for boolean functions. Imagine truth table with all variables. Each node is a variable, edge is either or . At the end, node is or . See Dragon §12.
• Limiting difference prop when adding edges
• Demand-driven analysis: only analyze where client requests it!

Access-path tracking

But there are some cases where we want must-alias analyses! For example, let’s look at the following example:

File makeFile() {
	return new File();
}
 
File f = makeFile();
File g = makeFile();
 
if (...) {
	f.open();
}

Let’s try to do state tracking. In points-to analysis, we have to represent both f and g with a single abstract object A, since they both call into makeFile. When we do f.open, A could be either closed or open, so we have to say A is both in an open state and in its initial state. This called a weak update—it maintains the old state as part of the updated state. But now we can’t really do any verification on this!

Note that context sensitivity doesn’t really help here—both have the same method call stack!

We want to do strong updates, where we decisively choose the new state of the abstract object. We need to know that f must point to a different object than g.

This approach combines may- and must-alias info, made for typestate verification.

Access paths

Danger

I’m not gonna reproduce the formal Greek here; this section just gives the general intuition for the technique.

An access path consists of all of x.y. ... .z.

First, we run flow-insensitive points-to analysis. Each abstract memory location in the points-to analysis—the mapped-to part of the analysis, not the variables or whatever—is referred to as an instance key.

Our analysis is flow-sensitive and context-sensitive. The analysis contains a bunch of abstract program states. Each of these states contains a bunch of tuples , where:

• is an instance key.
• indicates if the allocation site has a single concrete live object
• is all access paths that must point to
  • Has a length—maximal length of access path in this set—and a width—maximum number of access paths
• is a bool, indicating if there are access paths (not in ) that may point to .
• is all access paths that don’t point to .
  • Also has length and width

They define soundness on tuples and states to ensure that tuples (in a state) follow these rules.

At each statement, for each input tuple, we transform it into a number of output tuples and union.

Important high-level overview:

• If we’re allocating and we’ve already seen this allocation before (i.e., ” = Stmt S”—it’s already in our tuples and we’re back here again), we return two tuples:
  • One for the new allocated object (we always do this regardless of if we’ve seen this allocation)
  • One for the previously allocated object assigned to that variable, which has been shadowed at this variable/access path by the new assignment.
    • This makes it potentially not unique—if there was one variable that refers to this object, it’d be zero now!
• For v = null, for all objects in the state, every path that starts with v should be moved to “doesn’t point to,” since it’s null now!

Here’s an example, where denotes tuple with state (i.e., init, open, etc.).

We limit the length & width of or sets because:

• With recursion, access paths are boundless
• Loop-free code might inflate the sets way too large.

Analyzing modern Java programs

Points-to analysis difficulties

Points-to sucks for modern Java, because of big libraries and reflection.

With reflection, we can do meta-programming with string names of program constructs like classes or methods:

class Factory {
	Object make(String x) {
		return Class.forName(x).newInstance();
	}
}

From type-level to term-level with strings. Reflection. Now we have no idea what kind of object is being allocated here! There are some mitigations but…

• We could track string constants, but people often do string concat and stuff.
• We could look for typecasts and use that to guide analysis
  • But often programs don’t do typecasts! e.g., calling the reflection fn Method.invoke()
  • Or things made with reflection flow to interfaces which are implemented by many different types.

Under-approximation

In contexts like bug finding, we actually don’t need an over-approximate answer; instead, we can do under-approximation instead—return a subset of answers or locations that we know for sure are correct! Here, we don’t guarantee that our results are all of the issues or aliases; but we guarantee that if we find something, it’s definitely wrong.

For instance, we can use an under-approximation of the access path analysis to check for resource leaks. Here, our tuples are , where is some resource type. Additionally, we only generate tuples when acquiring , and delete tuples when releasing . A memory leak corresponds to —a resource still exists at , but there are no access paths that are guaranteed to point to .

An example of a non-leaky code-snippet:

In the true case of the branch, there is no analysis, since r is a must-alias to a resource and so cannot be null. When we get to release, since r must alias, we release and get it to the end safely.

Here’s an example of a leak, which occurs if the loop runs twice. On run 1, we acquire R, then go to the node, assigning . Then, we reacquire R, creating a new tuple and killing from the previous tuple, yielding . Then, when we get to again, we kill from that tuple, yielding . A leak!

For dealing with reflections, they also do domain-specific reflection modeling. By “domain,” we mean “web frameworks” or that sort of thing. Application/programming domain.