tipSurveyProgramSlicing1994

See also

2024-04-16 • CS 294, 13Tu – Program Slicing: https://www.ssw.uni-linz.ac.at/General/Staff/CS/Research/Publications/Ste99a.html ch 3, http://www.r-5.org/files/books/computers/compilers/writing/Keith_Cooper_Linda_Torczon-Engineering_a_Compiler-EN.pdf general

Overview

A program slice consists of the parts of a program that affect the values computed at some point of interest: a slicing criterion, which contains a program point and a set of variables we’re interested in. The parts of a program that affect this criterion is the program slice with respect to the criterion.

There are a couple axes on which slicing techniques vary:

• Does the slice by itself constitute an executable program?
• Is the slice static—computed without assuming anything about program input—or dynamic—computed with respect to a specific input?

Static slicing

We can compute static slices by determining transitively relevant statements via data flow and control flow dependencies—see 2024-04-16 • CS 294, 13Tu – Program Slicing—or we can state it as reachability in a program dependence graph (PDG)!

We can compute backwards slices (find all things that influence this criterion from earlier), as well as forwards slices (find all things influenced by this criterion ahead). Their computation is similar.

Dynamic slicing

We execute with respect to a specific variable assignment, and potentially a specific execution of a line. For instance, we might be interested in seeing “the first occurrence of statement on line in the history of the program.” Additionally, if we have multiple reassignments in a loop, but one overwrites the other, we’re only interested in seeing the actually relevant one.

Applications

This is §7, but I’ve moved it up here!

• Debugging and program analysis
  • If a program computes a wrong value for , the statements in the slice are (probably) to blame! (Or maybe you’re missing a statement)
  • Forward slicing: off-by-one errors, inspect parts of a program that might be affected by a proposed modification
  • Program dicing: “if is correct but isn’t, show statements that are in ‘s slice but not ‘s”
    • Doesn’t work if multiple bugs, or if programs are coincidentally correct
  • Can detect dead code - statements not affecting any output, uninit vars
  • Debugging with dynamic slices
    • Composing slices to zoom in on potential location of bug
    • Heuristics for selecting statements likely to be involved in a bug
    • Using flowback analysis - more general dynamic slicing
• Programming differencing (i.e., git diffs)
  • Find components reflecting changed behavior—where slices have changed
• Software maintenance
  • Decompose program into set of components—*decomposition slice
• Testing
  • If all def-use pairs occur in a successful test we say a program satisfies a data flow testing criteria
  • With slicing, we can go stronger: enforce that every def-use pair influences ≥1 output value! Output-influencing
• Compiler tuning
  • Use dynamic slicing to detect redundant CSE
• Parallelism?
  • Several program slices executed in parallel, then splice them together in I/O-respecting way
• Stuff with modules, etc.

Data dependence and control dependence

Here, we’re interested specifically about flow dependence (i.e., not output dependence or antidependence). A statement is flow dependent on if a value computed at is used at . Formally, this means that is a reaching definition at .

For a definition of control dependence, see Ferrante et al. With structured control flow, given an if or while, whatever statements are inside this level of if or while are control flow dependence on the predicate.

Methods for static slicing

Basic algorithms

We’re gonna look at a bunch of different algorithms that do the same thing but in different ways: static slicing of structured, single-procedure programs with scalar variables.

Dataflow equations

One way to define a static slice , a subset of program , with respect to a criterion is having two properties:

1. is a valid program.
2. Wherever halts for an input, also halts, computing the same values for all variables in whenever the statement corresponding to node is executed.

This algorithm performs two distinct steps:

• Trace data dependences. Requires iteration to fixpoint in the presence of loops.
• Trace control dependences. For relevant predicates, trace their dependences.
  • We need this because of our definition that slices must run and run equivalently

At a broad level, for a criterion with at program point with a set of variables , we perform a backwards dataflow analysis, where our analysis is the set of variables relevant to our slice. As we go backwards, if a relevant variable is defined at a statement, we replace that variable with the variables referenced in that definition. The predicate of a conditional statement is indirectly relevant if one if its statements is relevant. We must include the slice for the predicate in our overall slice.

Before analysis, we also note the statements that are control dependent on the current statement. If a statement is included in the slice, we must calculate include the slice of any predicates the statement is control dependent on.

This is the approach described in 2024-04-16 • CS 294, 13Tu – Program Slicing.

Information-flow relations

We can define some relations that make statements about the flow of information that can be used to compute slices, with respect to a (sequence of) statement(s) , a variable , and an expression (control predicate or rvalue) in :

• iff value of on entry to affects the value computed for .
  • Backward: if
• iff computed value for potentially affects value of on exit from .
  • Forward
• iff value for on entry to affects value of on exit from .

Let ; the set of all expressions in a statement with respect to variable where potentially affects the value of later on after .

To get a backwards slice, we replace all statements in with no expressions in with empty statements. This means that the expressions in don’t affect ‘s later value at all, so they can be deleted. This yields the slice with respect to ‘s final value.

Basically, build for all . Then, for the variable we care about, see if it’s in . If not, delete.

To get a slice at an arbitrary point, insert a dummy assignment v' = v somewhere and take the slice of v'.

Note

To get a forward slice, use instead of .

To define the relations, we pattern match (i.e., perform structural induction) on the statement . i.e., syntax-directed!

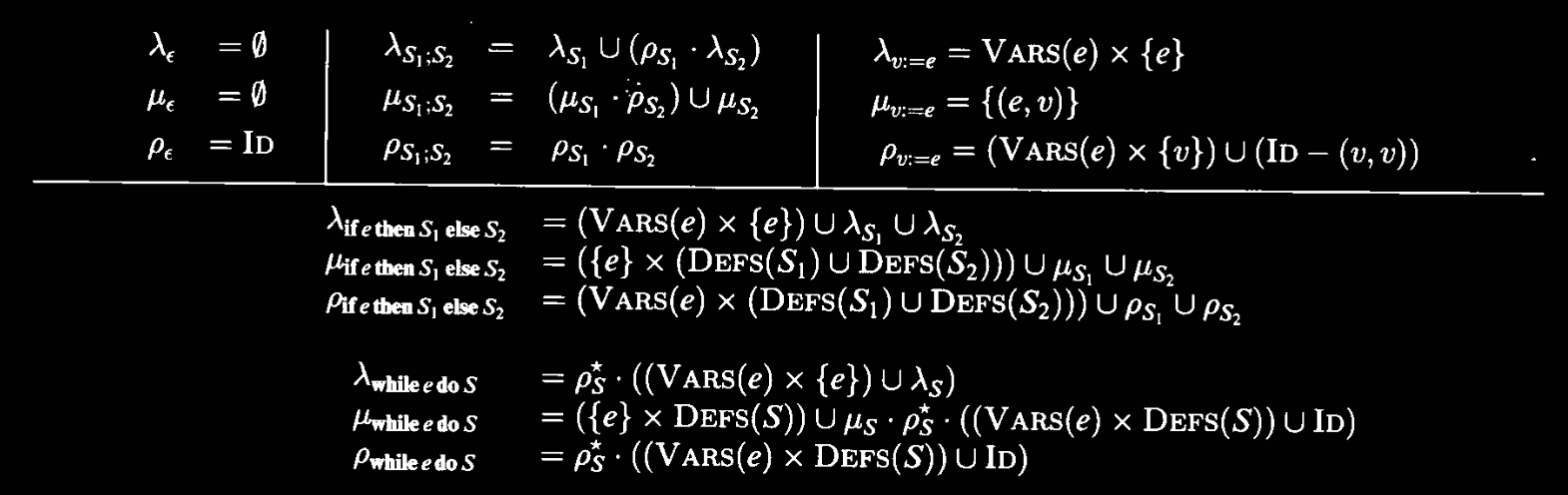
Brief summary:

• For
  • For sequencing, relation composition.
  • For assignment, value of vars in expression affects value of assigned var
    • Also, id, except for assigned var.
  • For conditionals, the vars in e could affect vars defined in and . And inherit branches, identity
  • For loops, the vars in e could affect vars defined in . Fixpoint.
• For
  • For sequencing, look at , and only look at variables that, coming from , could affect variables coming into . Combine this with whatever’s in .
  • For v := e, e is affected by all vars it references.
  • For if e then S1 else S2, eis affected by vars it references. Also include relations from S1 and S2.
• For
  • Sequencing: all the forward affects from , plus those from that are also changed on .
  • Assignment: affects on exit.
  • Conditional: predicate affects all defs in all branches. Also inherit branches
  • Loop: predicate affects all definitions in statements (control). Also, inherit , but after fixpoint and all vars in predicate to all defs in the statement.

Dependence graph approaches

Basically, use a PDG! There are some mods you can add on:

• Add nodes for program (sub)expressions
• Explicitly add file descriptors
• Add finer-grained dependences between individual variables defined/used at program points.
  • Vertexes are boxes with separate ports for each variable defined or used at that program point.
  • Every box has an port, representing “execution” of that statement, and control predicates have a port, for their temporary value, for control dependence purposes.
  • A slice criterion is now a pair of source and sink ports we’re interested in.

For multi-procedure programs

From notes:

Note: for interprocedural static slices, one can find the corresponding SDG = system dependence graph for multi procedure programs. Then, new dependence between input and output parameters of each procedure call are explicitly represented in the SDG (summary edges). Then a two pass algorithm is used to extract the slices from an SDG.

Methods for dynamic slicing

Basic algorithms

Dynamic flow concepts

The key sauce with dynamic flow concepts is that we want to distinguish between multiple executions of the same statement. This allows us to get more information, e.g., if an assignment is killed by a later execution of an assignment that occurs spatially earlier in the program source.

To do this, we formalize the notion of the execution history of a program as a trajectory. A statement occurrence stands for “the statement or control predicate , which was the th statement executed in our execution history.” A trajectory is just an execution history: a list of statements executed on this execution path.

A dynamic slicing criterion contains the input of the program , the statement occurrence we’re interested in evaluating at, and the variables we want a slice for. A dynamic slice in this setting has similar properties to static slices from dataflow:

1. With input , trajectory of is identical to trajectory of (where any statements not in are removed)
2. Identical values are computed for at .
3. must appear in .

To compute dynamic slices, we introduce three dynamic flow concepts; we call them these since these are kinda dataflow-y, but not exactly. It’s three analyses, in the form of syntax-directed relations, that we build about our program:

1. Definition-use (DU): to a use of a variable, from its most recent definition. i.e., from reaching definition to its use.
2. Test-control (TC): from most recent occurrence of control predicate, to statements control dependent on that occurrence of predicate
3. Identity (IR): different occurrences of the same statement.

Computing a set of statement occurrences to include in a slice is a fixpoint process. On each new iteration , we add occurrences that are in the from position of any relation where an item in is in the to position.

We need IR for termination in the presence of loops.

Dynamic dependence relations

How could we use a PDG to

• We could try marking vertices executed in a test set, and only include executed vertices in the slice. Imprecise: if there’s an edge between marked vertices, but definitions of aren’t used in , it’s still added.
• We could try marking executed edges, and only including items along marked edges. However, an edge traversed through one iteration will be present in all subsequent iterations, even if the same dependence doesn’t occur.
• The solution: create a distinct vertex in the PDG for each occurrence of a statement in the execution history.
  • Called a dynamic dependence graph (DDG). A criterion is an occurrence of a statement in the DDG.
  • This is similar to above!
  • Unfortunately, number of possible slices is .
  • Can compute a reduced dynamic dependence graph (RDDG): only add a new vertex if it can create a new dynamic slice.

Future work

There are two main constraints with slices as described here:

1. Slices must contain a subset of original program’s statements—and might need to be syntactically valid itself
   1. In some languages, you can’t have empty ifs. What then?
2. Slices are computed via data and control dependences
   1. If we do constant propagation in slicing (along with other program optimization techniques, e.g., symbolic execution), we might get smaller slices!
   2. Broadly, we can get this by transforming into IR, optimizing IR, maintaining mapping between source and (un)optimized IR, and getting slices from IR

Conclusion

We include this here to show what else we haven’t touched on:

• Interprocedural slicing
• Unstructured control flow
• Composite data types & pointers
• Concurrency